Курсовая работа: Обнаружение многопозиционного сигнала Баркера на фоне гауссовского шума
Прямое вычисление по формуле (1.2) становится слишком громоздким при большом числе позиций N многопозиционного сигнала u(t). В этом случае используем более простой метод, основанный на известных соотношениях и на скачкообразных изменениях сигнала Баркера:
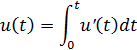
![]()
Тогда искомое преобразование Лапласа U(s) сигнала u(t) примет вид
![]()
где U'(s) - преобразование Лапласа производной u'(t).
Найдём преобразование Лапласа семипозиционного сигнала Баркера (рисунок 2) с амплитудой А и длительностью одной позиции τ.
В соответствии с предложенной методикой рассчитаем преобразование Лапласа.
![]()
Смоделируем источник кода Баркера в пакете OrCAD, (см. рисунок А.1). Проведя анализ сигнала во временной области в программе PSpice. Выведем в графическом модуле Prob результаты – рисунок 3. На рисунке 4 можно видеть частотный спектр сигнала Баркера.
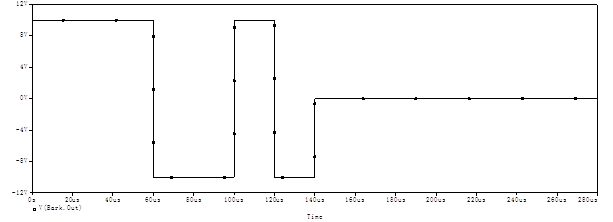
Рисунок 3 – Сигнал Баркера

Рисунок 4 – Спектр сигнала Баркера
2. ФАЗОВЫЙ МАНИПУЛЯТОР
Для передачи многопозиционных сигналов по радиоканалу используются дискретные виды модуляции, когда амплитуда, фаза или частота высокочастотной синусоидальной несущей меняется скачком под воздействием модулирующего сигнала u(t), т.e. имеют место, соответственно, амплитудная манипуляция (АМн), фазовая манипуляция (ФМн) и частотная манипуляция (ЧМн).
АМн используется при однополярном модулирующем сигнале типа кода Шермана, а ФМн и ЧМн применяются для передачи биполярных сигналов.
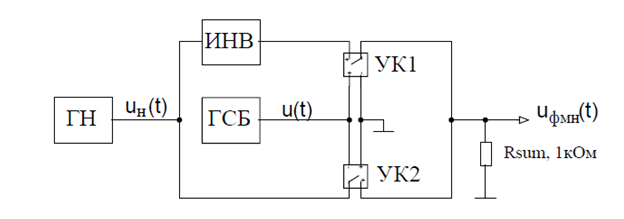
Рисунок 5 – Структурная схема ФМн модулятора
Наиболее распространенная схема фазового манипулятора состоит из генератора несущего колебания, несущая частота подается на два ключа в прямом состоянии, и на второй после инверсии, происходит смена фазы(см рисунок 5).
Схема фазового манипулятора, спроектированная в OrCAD, представлена на рисунке 6.
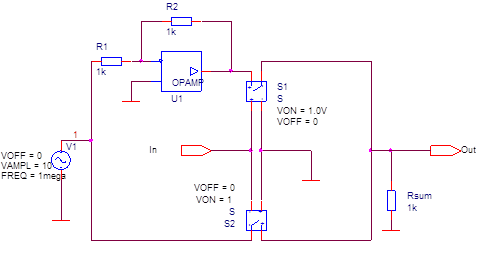
Рисунок 6 – Фазовый манипулятор
Принципиальная схема модулятора представлена в приложении на рисунке А.6
Промодулированный сигнал представлен на рисунке 7. Для большей наглядности на рисунке 7 так же показан его спектр и спектры (сверху вниз):колебания генератора,входного сигнала,выходного сигнала.
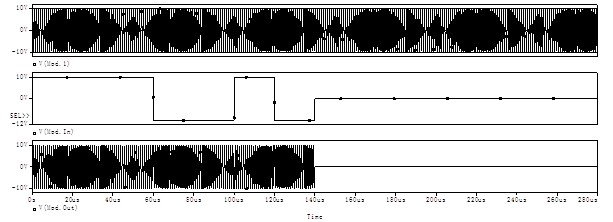
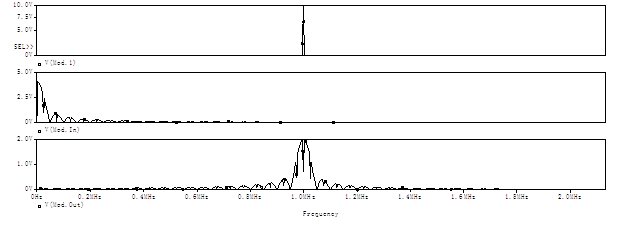
Рисунок 7 – Временные зависимости и спектры модулированного колебания.
3. КАНАЛ СВЯЗИ
При прохождении сигнала в среде распространения на него накладываются высокочастотные шумы. В результате детектирование полезного сигнала в смеси сигнал-шум становится затруднено.
Шум, присутствующий в канале связи, обычно распределен по закону Гаусса. Кроме того, ширина спектральной области, занимаемая шумом, значительно превосходит ширину спектра полезного сигнала. С учетом этих факторов сигнал на выходе имитатора канала связи с шумом представим в следующем виде:
где umod (t) –сигнал с выхода модулятора
n(t) –высокочастотный нормальный случайный процесс (шум).
Шумовой процесс, в свою очередь, можно разложить на два.
![]()
Здесь ξ1 и ξ2 –низкочастотные некоррелированные нормальные случайные процессы,
ω0 – центральная частота спектра шума n(t).
Таким образом, можно смоделировать условия прохождения сигнала через канал связи. Схема шумового воздействия представлена в приложении на рисунке А.3. Результаты расчета в OrCAD представлены на рисунках 8-9.

Рисунок 8 – Сигнал после прохождения через канал передачи
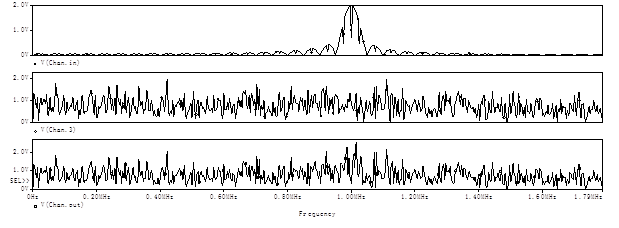
Рисунок 9 – Спектр сигнала после прохождения через канал передачи
4. ДЕМОДУЛЯТОР
ФМн-демодулятор (рисунок 10) состоит из полосового фильтра ПФ, настроенного на несущую частоту f0=1МГц,генератор опорного напряжения ГОН, который формирует синусоидальное колебание с амплитудой, частотой и начальной фазой, равными соответствующим параметрам сигнала с выхода ПФ. Принимаемое и опорное колебания складываются в сумматоре С и вычитаются в вычитающем устройстве ВУ1 так, что на входе нелинейной цепи НЦ1 имеем сумму Uпф(t)+Uoп(t), а на входе нелинейной цепи НЦ2 - разность Uпф(t)-Uoп(t). Далее сигнал с выхода НЦ2 вычитается из сигнала с выхода НЦ1 и разностный сигнал проходит через фильтр нижних частот ФНЧ, где и выделяется низкочастотный сигнал.
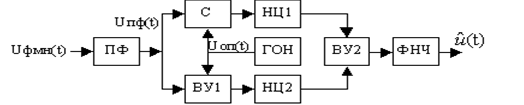
Рисунок 10 – Структурная схема ФМн-демодулятора
Для настройки ПФ проведем расчет фильтра в частотной области, и выведем АЧХ ПФ. Для численного контроля симметрии полученной АЧХ относительно частоты f0 применим функцию измерений B2freq.
Значение целевой функции B2freq близко к нулю, если форма АЧХ симметрична. Можно добиться такого результата, если подобрать соответствующее значение параметра B резонансного усилителя U2 (U2.B) в режиме оптимизации. При этом все остальные параметры усилителей U1 и U2 остаются фиксированными.
Цель оптимизации – найти такие значения варьируемых значений B и KFR. При оптимизации используется метод наискорейшего спуска, изложенный ниже в сравнении с методами градиента и методом релаксаций.