Курсовая работа: Обнаружение многопозиционного сигнала Баркера на фоне гауссовского шума
Метод релаксаций обладает в этом смысле определенными преимуществами, т.к. при спуске вдоль выбранного осевого направления не требуется вычисления производных. Но движение происходит не в оптимальном направлении.
Сочетание основных идей методов релаксации и градиента дает метод наискорейшего спуска, суть которого заключается в следующем.
После того, как в начальной точке найден градиент оптимизируемой функции и тем самым определено направление ее наибыстрейшего убывания, то в случае поиска минимума целевой функции в данном направлении делается шаг спуска. Если значение целевой функции в результате шага уменьшилось, то производится очередной шаг в этом направлении, и так до тех пор, пока в этом направлении не будет найден минимум целевой функции. После этого вычисляется градиент и определяется новое направление наибыстрейшего убывания целевой функции.
В сопоставлении с методом градиента метод наискорейшего спуска оказывается более выгодным из-за сокращения объема вычислений. По сути, метод наискорейшего спуска по вычислительным затратам эквивалентен методу релаксации, но выгодно отличается от него тем, что по крайней мере первые шаги после определения градиента производятся в оптимальном направлении.
Очевидно, что чем менее резко изменяется направление градиента целевой функции, тем выгоднее использовать метод наискорейшего спуска по сравнению с методом градиента (т.е. вдали от точки оптимума). Вблизи оптимума направление градиента меняется резко, поэтому метод наискорейшего спуска автоматически переходит в метод градиента, т.к. минимум по каждому направлению находится за небольшое количество шагов
Важной особенностью метода наискорейшего спуска является то, что при его применении каждое новое направление ортогонально предыдущему. Это объясняется тем, что движение в одном направлении производится до тех пор, пока направление движения не окажется касательным к какой-либо линии постоянного уровня (так же как и в методе релаксации). Но в отличие от метода релаксации скорость сходимости к точке оптимума не зависит от ориентации системы координат.
В качестве критерия окончания поиска могут использоваться те же условия, что и в методах релаксации и градиента.
После проведения оптимизации для обоих фильтров, проведем еще раз анализ ПФ1 и ПФ2 в частотной области. Результат показан в линейном масштабе на рисунке 11.

Рисунок 11 – АЧХ полосового фильтра
После моделирование схемы демодулятора представленной в приложении Б.4. На выходах блоков демодуляторов получили следующие временные и частотные диаграммы (см. Рисунки 12 – 13).
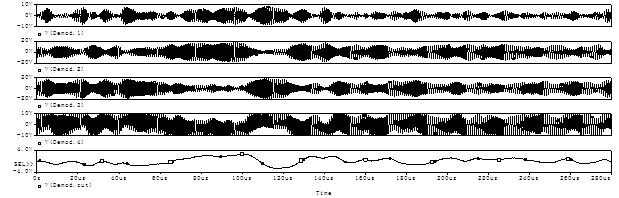
Рисунок 12 – Сигнал после детектирования
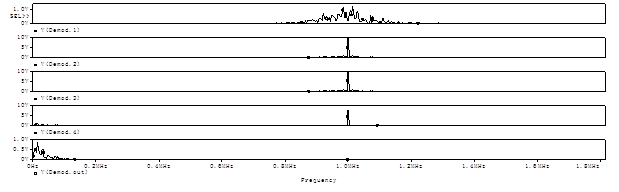
Рисунок 13 – Спектры сигнала после детектирования
5. СОГЛАСОВАННЫЙ ФИЛЬТР
цифровой код баркер гауссовский шум
Согласованный (оптимальный) фильтр максимизирует отношение сигнал/шум на своём выходе. Структура СФ в общем случае определяется сигналом Баркера u(t) и вероятностными характеристиками шума n(t). Так, если на входе СФ действует аддитивная смесь: x(t)=u(t)+n(t), где n(t) - гауссовский белый шум, то комплексный коэффициент передачи G(jω) и импульсная характеристика g(t) фильтра имеют вид [1]:
G(jω)=kU*(jω)еxp(-jωt0 )
g(t)=ku(t0 -t)
Здесь U*(jω) - комплексно-сопряженная спектральная плотность сигнала u(t);
k -коэффициент усиления СФ, задаваемый произвольно;
t0 -временная задержка фильтра, определяемая из условия физической реализуемости:
g(t)=0, t<0 (5.1.)
Условие (5.1.) означает, что отклик фильтра на произвольное входное воздействие не может появиться раньше этого воздействия. Обычно выбирают t0 =Т=Nτ - длительность сигнала u(t). Рассмотрим некоторые свойства CФ.
1 - Сигнал на выходе фильтра, согласованного с входным сигналом u(t), совпадает по форме с автокорреляционной функцией (АКФ) этого сигнала, сдвинутой по оси времени на величину t0 . Это непосредственно следует из подстановки импульсной характеристики и сигнала u(t) в интеграл Дюамеля, связывающего выходной сигнал с импульсной характеристикой g(t) и входным сигналом u(t). Таким образом, выходной сигнал в момент t=t0 имеет максимум, пропорциональный энергии входного сигнала u(t).
2 - Импульсная характеристика g(t) СФ при t0 =0 является зеркальным отображением сигнала u(t)
Что бы синтезировать фильтр необходимо. Найти передаточную функцию СФ. Произведем это по формуле 5.2.:
![]() (5.2.)
(5.2.)
В результате получим выражение:
![]()
По передаточной функции построить принципиальную схему состоящую их линий задержек и суммирующего устройства (См. рисунок А.4).
Проанализируем схему, подключив к входу сигнал Баркера. В результате получим на выходе АКФ сигнала, сдвинутую на время задержки. Результат представлен на рисунке 14.

Рисунок 14 – Реакция СФ на подачу сигнала Баркера
Теперь можно подключить к входу СФ всю остальную модель. Получим следующие графики (см. рисунки 13 – 14)

Рисунок 16 – Сигнал на выходе СФ

Рисунок 17 – Спектр сигнала на выходе СФ
6. РЕШАЮЩЕЕ УСТРОЙСТВО
Решающее устройство предназначено для формирования импульса прямоугольной формы момент, когда напряжение с выхода СФ превысит заданный пороговый уровень Unop. Факт наличия прямоугольного импульса на выходе РУ свидетельствует об обнаружении сигнала.
В качестве РУ обычно используют операционные усилители в нелинейном режиме, триггеры Шмитта и компараторы. В настоящей курсовой работе применим схему РУ на компараторе K521CA2 в интегральном исполнении.
Принципиальную схему см. рисунок А.5.