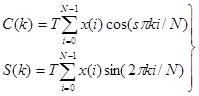Курсовая работа: Обработка данных в автоматизированных системах

2.2 Спектральный анализ на основе преобразования Фурье

Дискретное преобразование Фурье (финитное) определяется следующим соотношением:

(2.2)

где X(k) - значение (комплексное) дискретного преобразования Фурье, определенное в частоте с номером k;

x(i) - значение (вещественное) исходного временного ряда, определенное в момент времени с номером i;

T - период дискретизации;

N - количество отсчетов (длина) временного ряда.

Дискретное преобразование Фурье связывает спектральную характеристику (комплексный спектр) X(k), определенную в дискретных значениях частоты (с номером k), с дискретными значениями временного ряда (сигнала) x(i), определенными в дискретные моменты времени (с номером i).

Точность представления спектральной характеристики определяется разрешением по частоте:

(2.3)

Обратное дискретное преобразование Фурье определяется следующим соотношением:

(2.4)

Из сравнения формул (2.2) и (2.4) следует, что они отличаются знаком показателя экспоненты, множителем перед знаком суммы, а также переменной суммирования. Это позволяет строить единые программы для прямого и обратного преобразований Фурье.

Применяя формулу Эйлера, выражение (2.2) можно привести к виду:

(2.5)

где

(2.6)

Оценивание спектральной плотности мощности (СПМ) с помощью дискретного преобразования Фурье осуществляется по формуле:

(2.7)

где X(k) - дискретное преобразование Фурье (спектральная характеристика) временного ряда , соответствующего процессу x(t), обладающего свойством эргодичности;

T - период дискретизации процесса x(t);

N - длина временного ряда.

Черта в правой части формулы (2.7) означает операцию осреднения. Применение формулы (2.7) без операции осреднения приводит к получению "грубой" оценки СПМ. Формула (2.6) позволяет вычислить оценку СПМ посредством статистического осреднения модуля спектральной характеристики совокупности данных, поделенного на длину записи данных. Статистическое осреднение необходимо здесь потому, что ординаты спектральной характеристики являются случайными величинами, изменяющимися для каждой используемой реализации случайного временного ряда .

Операция осреднения уменьшает статистическую изменчивость, или повышает статистическую устойчивость. В спектральном анализе случайных временных рядов на статистическую устойчивость влияют два параметра - разрешение по частоте и длина записи .

Можно показать, что оценки ПСМ приближенно имеют распределение с n степенями свободы, где . Более того, для достаточно больших n, например, , распределение аппроксимируется гауссовским (нормальным) распределением. В этом случае нормированное стандартное отклонение (стандартное отклонение, связанное с оцениваемой величиной, т.е. процентная ошибка, или, в статистической терминологии, "коэффициент разброса") определяется соотношением:

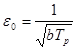(2.8)

Величину называют стандартной ошибкой. Если , то

.

Результат означает, что вычисление оценки СПМ с использованием полной длины временного ряда имеет стандартную ошибку, равную 100%.

Если отрезок поделить на m участков, то в этом случае:

(2.9)

Подставляя полученный результат в (2.7), найдем:

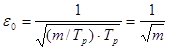(2.10)

Таким образом, для повышения точности оценивания СПМ необходимо исходный временной ряд длины N разбить на m участков длины Nу, вычислить для каждого i-го участка по формуле (1), а затем найти осредненную оценку по формуле:

(2.11)

Следует иметь в виду, что разрешение по частоте в рассмотренном случае определяется из соотношения . Число степеней свободы для найденной оценки СПМ можно найти следующим образом:

(2.12)

Следовательно, для повышения степеней свободы и, соответственно, статистической устойчивости оценок СПМ необходимо увеличивать число участков для осреднения.