Курсовая работа: Однопроходный/двухпроходный транслятор с языка математических выражений на язык деревьев вывода
Далее следует представление простого шаблона, составляющего регулярное выражение, которое ищет идентификаторы. Lex читает этот шаблон и создает C код для лексического анализатора, который ищет идентификаторы.
letter (letter|digit)*
Этот шаблон ищет строку символов, которая начинается с единичного символа, следующим за нулем или больше символов или цифр. Этот пример хорошо иллюстрирует, операции, разрешенные а регулярных выражениях:
• повторение, представленное оператором «* » (repetition)
• чередование, представленное оператором «| » (alternation)
• объединение (concatenation)
Любое регулярное выражение может быть представлено автоматом с конечным числом состояний (finitestateautomaton, FSA). Мы можем представить FSA, использующее состояния и переходы между состояниями. Существует одно начальное состояние и одно, или больше, конечных состояний или разрешенных состояний.
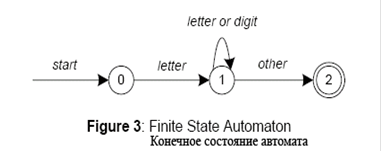
На рис. 3, состояние 0 – является начальным состоянием, а состояние 2 – разрешенным состоянием. Когда происходит чтение символа, осуществляется переход из одного состояния в другое. Когда читается первый символ, осуществляется переход в состояние 1. Автомат остается в состоянии 1, пока читаются буквы (letters) или цифры (digits). Когда осуществляется чтение иного символа, кроме буквы или символа, осуществляется переход в состояние 2, разрешенное состояние. Любой FSA может быть представлен с помощью компьютерной программы. Например, этот автомат с 3 мя состояниями программируется следующим образом:
start: goto state0
state0: read c
if c = letter goto state1
goto state0
state1: read c
if c = letter goto state1
if c = digit goto state1
goto state2
state2: accept string
Это техника, используемая lex. Регулярные выражения транслируются с помощью lex в компьютерную программу, которая реализует FSA. Используя следующий входной символ и текущее состояние, следующее состояние определяется с помощью индексирования в сгенерированной компьютером таблице состояний.
Теперь становится легко понять ограничения в lex. Например, lex не может быть использован.
Таблица 1. Элементарныешаблоны (Pattern Matching Primitives)
| Метасимвол (Metacharacter) | Совпадения (Matches) |
| . | Любой символ, кроме перевода строки |
| \n | Символ перевода строки |
| * | 0 или более копий предшествующих выражений |
| + | 1 или более копий предшествующих выражений |
| ? | 0 или 1 копия предшествующих выражений |
| ^ | Начало строки |
| $ | Конец строки |
| a|b | a илиb |
| (ab)+ | Одна или более копийab (группировка, grouping) |
| «a+b» | литерал«a+b » (C escapes still work) |
| [] | Класс символов |
Таблица 2. Примеры шаблонов выражений (PatternMatchingExamples)
| Выражение (Expression) | Совпадения (Matches) |
| abc | abc |
| abc* | ab abc abcc abccc… |
| abc+ | abc abcc abccc… |
| a(bc)+ | abc abcbc abcbcbc… |
| a(bc)? | a abc |
| [abc] | Одно из: a , b , c |
| [a-z] | Любой символ, a-z |
| [a\-z] | Одно из: a , - , z |
| [-az] | Одно из: - , a , z |
| [A-Za-z0–9]+ | Один или более символов алфавита или цифр |
| [\t\n]+ | Пробельные символы |
| [^ab] | Все, кроме: a , b |
| [a^b] | Одно из: a , ^ , b |
| [a|b] | Одно из: a , | , b |
| a|b | Одно из: a , b |
Регулярные выражения в lex составляются из метасимволов (Таблица 1). Примеры совпадения шаблонов показаны в таблице 2. При использовании класса символов, обычные операторы теряют свое назначение.
Следующие два оператора разрешены в классе символов: дефис («–», hyphen) и циркумфлекс («^ », circumflex). При использовании между двумя символами дефиса, представляется диапазон символов. Циркумфлекс, при использовании его как первого символа, отрицает выражение. Если два шаблона совпадают с некоторой строкой, используется наиболее шаблон, по которому найдена наиболее длинная строка, в случае, если длина одинакова, используется первый шаблон.
… definitions…
%%
… rules…
%%
… subroutines…