Математика / Курсовая работа: Оператор сдвига

Курсовая работа: Оператор сдвига

Теорема 2 [1]. Для любого ограниченного оператора А , действующего из нормированного пространства в нормированное .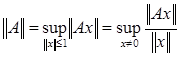

3. Сумма и произведение линейных операторов. Пространство линейных непрерывных операторов

Определение 4. Пусть А и В – два линейных оператора, действующих из линейного топологического пространства Е в пространство Е1. Назовем их суммой А+В оператор С, ставящий в соответствие элементу элемент у=Ах+Вх, .

Можно проверить, что С=А+В – линейный оператор, непрерывный, если А и В непрерывны. Область определения DC оператора С есть пересечение областей определения операторов А и В.

Если Е и Е1 – нормированные пространства, а операторы А и В ограничены, то С тоже ограничен, причем

(2)

Действительно, для любых х , следовательно, выполняется неравенство (2).

Определение 5. Пусть А и В – линейные операторы, причем А действует из Е в Е1, а В действует из Е1 в Е2 . Произведением ВА операторов А и В называется оператор С, ставящий в соответствие элементу элемент из Е2.

Область определения DC оператора С=ВА состоит из тех хDA , для которых АхDB. Ясно , что оператор С линеен. Он непрерывен, если А и В непрерывны.

Если А и В – ограниченные операторы, действующие в нормированных пространствах, то и оператор С=ВА – ограничен, причем

(3)

Действительно, , следовательно, выполняется (3).

Сумма и произведение трех и более операторов определяются последовательно. Обе эти операции ассоциативны.

Произведение оператора А на число к (обозначается кА) определяется как оператор, который элементу х ставит в соответствие элемент кАх.

Совокупность Z(E,E1) всех непрерывных линейных операторов, определенных на всем Е и отображающих Е в Е1 ( где Е и Е1– фиксированные линейные нормированные пространства), образует, по отношению к введенным операциям сложения и умножения на число, линейное пространство. При этом Z(E, E1) – нормированное пространстово (с тем определением нормы оператора, которое было дано выше).

4. Обратный оператор

Пусть А – линейный оператор, действующий из Е в Е1 , и DA область определения, а RA – область значений этого оператора.

Определение 6. Оператор А называется обратимым, если для любого уRA уравнение Ах=у имеет единственное решение.

Если А обратим, то любому элементу уRA можно поставить в соответствие единственный элемент хDA , являющийся решением уравнения Ах=у. Оператор, осуществляющий это соответствие, называется обратным к А и обозначается А-1.

Теорема 3 [1]. Оператор А-1, обратный линейному оператору А, также линеен.

Доказательство.

Достаточно проверить выполнение равенства