Курсовая работа: Оператор сдвига
Теорема 8. Оператор двухстороннего сдвига является унитарным оператором
Доказательство. Рассмотрим оператор двустороннего сдвига
U(…, x-1, x00, x1, …)=(…, x-2, x-10, x0, x1, …).
Очевидно, что этот оператор сохраняет норму, т.е. является изометрическим: ![]() . Покажем, что он имеет обратный оператор – это оператор, который любую последовательность сдвигает влево.
. Покажем, что он имеет обратный оператор – это оператор, который любую последовательность сдвигает влево.
В пространстве последовательностей, как и в любом метрическом пространстве, любой вектор представляется как линейная комбинация элементов базиса. В этом пространстве имеется канонический базис – это последовательности вида
………………………
l-1=(.., 0, 1-1, 0, …)
l0=(…, 0, 10, 0, …)
l1=(…, 0, 11, 0, …)
………………………
Подействуем оператором U на произвольный элемент базиса:
Ulk=U(…, 0, 1k, 0,…)=(…, 0, 1k+1, 0)=lk+1.
Т.е. каждый элемент базиса оператор U переводит в последующий элемент. Чтобы осуществлялось обратное действие, мы должны каждый элемент базиса перевести в предыдущий элемент, т.е. U-1lk=lk-1.
Каждый вектор пространства l2 х=(…, х-1, х0, х1, …) может быть представлен в виде: ![]() . А так как оператор U-1 элементы базиса переводит в предыдущие, то, действуя на последовательность
. А так как оператор U-1 элементы базиса переводит в предыдущие, то, действуя на последовательность ![]() , сдвинет ее влево.
, сдвинет ее влево.
Итак, мы получили, что оператор двухстороннего сдвига U имеет обратный оператор и является изометрическим, следовательно, он является унитарным. Спектр этого оператора лежит на единичной окружности.
7.Взвешенные сдвиги
Определение 12. Оператором взвешенного сдвига называется произведение оператора сдвига (одностороннего или двустороннего) на диагональный (в этом же базисе) оператор.
Более подробно: пусть ![]() – ортонормированный базис (n = 0, 1, 2, … или n = 0,
– ортонормированный базис (n = 0, 1, 2, … или n = 0, ![]() 1,
1, ![]() 2, …) и пусть
2, …) и пусть ![]() – ограниченная последовательность комплексных чисел (n пробегает те же значения, что и выше). Оператором взвешенного сдвига называется оператор вида SP, где S– оператор сдвига (Sln= ln+1) ,а Р – диагональный оператор с диагональю
– ограниченная последовательность комплексных чисел (n пробегает те же значения, что и выше). Оператором взвешенного сдвига называется оператор вида SP, где S– оператор сдвига (Sln= ln+1) ,а Р – диагональный оператор с диагональю ![]() (Pln =
(Pln = ![]() ln ).
ln ).
Найдем выражение для нормы и спектрального радиуса оператора взвешенного сдвига через его веса.
Вспомним, что сдвиг S1 – изометрический оператор, значит, не изменяет нормы элемента: ![]() для любого
для любого ![]() .Поэтому норма оператора А равна норме соответствующего диагонального оператора: для любого
.Поэтому норма оператора А равна норме соответствующего диагонального оператора: для любого ![]()
![]() и
и ![]() . Найдем норму диагонального оператора Pln =
. Найдем норму диагонального оператора Pln = ![]()
![]() , где
, где ![]() – некоторая ограниченная последовательность комплексных чисел. Рассмотрим произвольную последовательность
– некоторая ограниченная последовательность комплексных чисел. Рассмотрим произвольную последовательность ![]() с единичной нормой:
с единичной нормой: 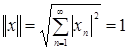 . При этом в базисе
. При этом в базисе ![]() элемент
элемент ![]() имеет разложение
имеет разложение 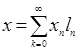 . Подействуем на элемент х оператором Р:
. Подействуем на элемент х оператором Р: 
 . При этом
. При этом 
![]()
![]()

![]() . Отсюда следует, что
. Отсюда следует, что ![]()
![]() . Покажем, что выполняется также и обратное неравенство. Если для последовательности
. Покажем, что выполняется также и обратное неравенство. Если для последовательности ![]()
![]() достигается, т.е.
достигается, т.е. ![]() при некотором
при некотором ![]() , то возьмем элемент
, то возьмем элемент ![]() :
: ![]()
![]() ,
, ![]()
![]() . Если же
. Если же ![]() не достигается, то можно взять подпоследовательность
не достигается, то можно взять подпоследовательность ![]()
![]() , тогда
, тогда ![]()
![]() . Это говорит о том, что не может быть
. Это говорит о том, что не может быть ![]()
![]() . Итак,
. Итак, ![]()
![]() и
и ![]()
![]() . Мы получили, что норма оператора взвешенного сдвига равна точной верхней грани модулей его весов.
. Мы получили, что норма оператора взвешенного сдвига равна точной верхней грани модулей его весов.
Чтобы найти спектральный радиус оператора взвешенного сдвига, найдем нормы его степеней. Вычислим степени оператора А: Aln = ![]() , A2ln =
, A2ln = ![]() ,A3ln =
,A3ln = ![]() , и так далее. Следовательно, Ак можно представить в виде произведения изометрии (к-й степени оператора сдвига) и диагонального оператора, у которого n-й диагональный член равен произведению к последовательных чисел
, и так далее. Следовательно, Ак можно представить в виде произведения изометрии (к-й степени оператора сдвига) и диагонального оператора, у которого n-й диагональный член равен произведению к последовательных чисел ![]() , начиная с
, начиная с ![]() . Значит,
. Значит,  , отсюда,
, отсюда,  .
.
8. Операторы сдвига в пространстве функции на единичной окружности
Рассмотрим единичную окружность на комплексной плоскости, т. е. всевозможные комплексные числа ![]() , по модулю равные 1. Рассмотрим комплексную последовательность
, по модулю равные 1. Рассмотрим комплексную последовательность ![]() и составим ряд
и составим ряд ![]() . Если он сходится для всех
. Если он сходится для всех ![]() , таких, что
, таких, что ![]() , то
, то ![]() – функция от переменной
– функция от переменной ![]() , определенная на единичной окружности. Заметим, что для последовательностей из пространства
, определенная на единичной окружности. Заметим, что для последовательностей из пространства ![]() , таких, что ряд
, таких, что ряд ![]() сходящийся, ряд
сходящийся, ряд ![]() сходится для всех
сходится для всех ![]() , таких, что
, таких, что ![]() . Итак, существует взаимно однозначное соответствие
. Итак, существует взаимно однозначное соответствие ![]() между пространством
между пространством ![]() и множеством A функций на единичной окружности, представимых в виде суммы обобщенного степенного ряда с абсолютно сходящимся рядом коэффициентов. Рассмотрим, в какой оператор переходит при этом оператор сдвига U. Обозначим этот оператор
и множеством A функций на единичной окружности, представимых в виде суммы обобщенного степенного ряда с абсолютно сходящимся рядом коэффициентов. Рассмотрим, в какой оператор переходит при этом оператор сдвига U. Обозначим этот оператор ![]() . Пусть
. Пусть ![]() и
и ![]()
![]() – соответствующая функция. Тогда
– соответствующая функция. Тогда ![]()
![]()
![]() . Итак, в пространстве А оператору сдвига соответствует оператор умножения на функцию
. Итак, в пространстве А оператору сдвига соответствует оператор умножения на функцию ![]() .
.
Рассмотрим теперь оператор