Курсовая работа: Определение оптимальных складских запасов

Обозначим

, (3)

Получим

. (4)

Подставляя (4) в (1.1), получаем

(5)

Найдем выражение для функции затрат с учетом (4), (5):

. (6)

Для нахождения средних затрат в единицу времени, поделим функцию затрат L _T на период времени Т :

. (7)

Теперь нужно найти такие значения Y ₀ , T ₀ , для которых функция L _ср минимальна. Для этого составляем и решаем систему уравнений из частных производных функции средних затрат в единицу времени L _ср по предельному запасу Y и по периоду времени Т :

Получим из первого уравнения системы и приравняем к нулю:

. (8)

Из второго аналогично:

. (9)

Из (8) получим такое соотношение

. (10)

Наконец, из (9) получим

. (11)

Подставляя в уравнение (11) выражение для Т из (10), после несложных преобразований получим

(12)

Подставив в (12) выражение для a из (3) и поделив числитель и знаменатель на λР , получим окончательное выражение для оптимального уровня запаса

; (13)

Подставив это выражение в (10), находим оптимальный период поставки

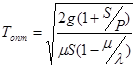. (14)

При таких значениях Y ₀ , T ₀ , достигается минимум средних расходов в единицу времени:

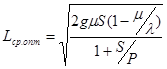. (15)

Рассмотрим теперь частные случаи общей задачи: