Курсовая работа: Определение оптимальных складских запасов

Рис. 3. График изменения запасов в случае, когда недостаток запасов не допустим

Если дефицит запасов недопустим значит, что удельный штраф за дефицит единицы продукта в единицу времени Р = ∞ и подставив S/ P =0 в (13) - (15), получим:

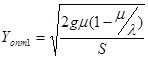, (16)

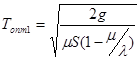,(17)

; (18)

2) мгновенные поставки (рис. 4).

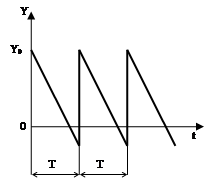
Рис. 4. График изменения запасов при мгновенных поставках

Мгновенные поставки означают, что λ = ∞ и μ/λ = 0. Теперь подставим в уравнения (13) - (15), получим

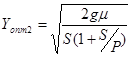, (19)

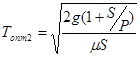,(20)

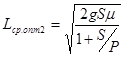; (21)

3)дефицит не допускается, поставки мгновенные (рис. 5).

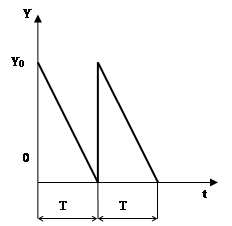
Рис. 5. График изменения запасов в случае, когда не допускается дефицит и поставки мгновенные

Данный частный случай является комбинированным из первого и второго пунктов, которые рассмотрены выше. Подставив Р = ∞ и S/ P =0, λ = ∞ и μ/λ = 0 в (13) - (15), получим

, (22)

,(23)

; (24)

Соотношения (22) – (24) называются формулами Уилсона, а (22) - экономическим размером партии.

4. Реализация найденного решения на практике

Задача управления запасами, а именно выбранная мною модель реализована в MathCad 2001iProfessional.

Список литературы

1. Черногородова Г.М. Теория принятия решений: Конспект лекций. Ч.1. Екатеринбург: Изд-во УМЦ УПИ, 2001. 97с.

2. Ю.П. Зайченко. Исследование операций. Учебник. - 6-е изд. Киев: Изд. дом: «Слово», 2003. 688с.

3. Задачи по исследованию операций. http://www.allmath.ru/appliedmath/operations/problems-tgru/zadachi.htm

4. Исследование операций: методы и модели. http://ecocyb.narod.ru/317/begin.htm

5. Электронное учебное пособие по курсу: «Моделирование экономических процессов». http://www.usfeu.ru/general_info/faculties/feu/metod/0611/Ush_posobie/Mep/ModEcProc/ras2.html

6. Википедия. Свободная энциклопедия. http://ru.wikipedia.org