Курсовая работа: Оптимизация алгоритмов поиска

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования "Воронежский государственный технический университет"

Радиотехнический факультет

Кафедра радиотехники

Специальность 210302 "Радиотехника"

Оптимизация алгоритмов поиска

Выполнил студент гр. РТ-041 Д.С. Чёткин

Проверил доцент кафедры В.П. Литвиненко

Воронеж 2007

Содержание

Введение. 4

1. Разработка оптимального дихотомического алгоритма поиска при равновероятном распределении вероятностей и числе событий М=16. 5

2. Разработка оптимального алгоритма поиска для экспоненциального закона распределения вероятностей при М=16. 7

3. Разработка оптимального алгоритма поиска экспоненциального закона распределения при числе измерений от N=15 до N=log2M.. 9

4. Разработка оптимального алгоритма поиска для 9-го варианта распределения при числе измерений от N=1 до 15. 12

Заключение. 19

Список литературы.. 20

Введение

Скрытность характеризует затраты (времени, средств), необходимые для выявления реасобытия с заданной достоверностью (вероятностью правильного решения, доверительной вероятностью ).

При формировании оценки скрытности случайного события в качестве оправной принята двухальтернативная пошаговая поисковая процедура, сущность которой заключается в следующем.

Множество Х с соответствующим законом распределения вероятностей разбивается на два подмножества и (верхний индекс - номер разбиения). Двоичный измеритель проводит двоичное измерение, выявляя, в каком подмножестве находится реасобытие (его след). Затем подмножество, в котором обнаружено реасобытие (на рис.2.1. это ), вновь разбивается на два подмножества и и выявляется след реасобытия в одном из них. Процедура заканчивается, когда в выделенном подмножестве оказывается одно событие. Поиск может быть последовательным и дихотомическим. В первом алгоритме () производится последовательный перебор состояний от первого до последнего, пока не встретится реасобытие.

Второй алгоритм поиска () предполагает разделение всего множества состояний пополам, проверку наличия реасобытия в каждой из этих частей, затем разделение выбранной половины множества X на две равные части с проверкой наличия в них реасобытия и так далее. Поиск заканчивается, когда в выделенном подмножестве оказывается одно событие.

Существует несколько способов минимизации двоичных поисковых процедур. Примерами могут служить методы Циммермана-Хафмена и Шеннона-Фоно. Оптимизировать алгоритм можно по различным параметрам с учетом стоимости измерения и без. В данной лабораторной работе исследовали оптимизацию дихотомического алгоритма поиска по наименьшей величине средней скрытности.

1. Разработка оптимального дихотомического алгоритма поиска при равновероятном распределении вероятностей и числе событий М=16

Включите режим дихотомического поиска. Установите число событий при равномерном распределении вероятностей и задайте число измерений . Разработайте оптимальный алгоритм поиска, задайте его на наборном поле, проведите моделирование, определите потенциальную скрытность.

В данном случае наиболее оптимальным алгоритмом поиска является алгоритм разработанный по принципу Шеннона-Фано. Данный метод предполагает исходное множество элементов с заданным распределением разбить на два подмножества с номерами 0 и 1 так, чтобы вероятности попадания в них были максимальны близки (в идеале пополам). Затем каждое из полученных подмножеств отдельно разбивается на два подмножества с тем же условием и номерами с 00,01,10,11. Разбиение заканчивается когда все элементы подмножества будут иметь только по одному элементу.

В результате разработан оптимальный алгоритм поиска для равновероятного закона распределения вероятностей.

Проведем расчет потенциальной скрытности для равновероятного закона распределения вероятностей:

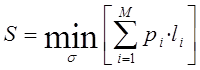(1)

В результате для данного случая:

В результате получено простое выражение для определения потенциальной скрытности равномерного закона распределения, который при дихотомическом алгоритме поиска не зависит от перебора комбинации измерений, а только от вида дерева поиска.

2. Разработка оптимального алгоритма поиска для экспоненциального закона распределения вероятностей при М=16

Выберите экспоненциальное распределение вероятностей событий вида , , - нормирующий множитель, при том же , что и в пункте 1. Определите оптимальный алгоритм поиска, задайте его на наборном поле, проведите моделирование, определите потенциальную скрытность.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--