Курсовая работа: Оптимизация алгоритмов поиска

Глядя на ход кривой снятия неопределенности приходим выводу, что ее ход является неоптимальным. Используя известные алгоритмы оптимизации поиска приходим к тому, что в данном случае оптимальным алгоритмом поиска является вовсе не дихотомический алгоритм при любых комбинациях нахождения реасобытия, а последовательный. Для данного случая он является оптимальным, так как первым измерением проверяется наиболее вероятное, затем следующее и так пока не останется неопределенности принятия решения.

Доказательство использования последовательного алгоритма поиска. Для этого используется метод Циммермана-Хаффмена. Данный метод оптимизации состоит из двух этапов: «Заготовительные операции» и «Считывание». Более подробно про это говорится в книге [1].

Так как показатель степени больше 1, а это удовлетворяет неравенству:

Где λ – показатель степени распределения вероятностей, равный 1, то для данного случая оптимальным является последовательный алгоритм поиска.

В результате выполнения данного пункта показано, что оптимальным является последовательный алгоритм поиска. Сравнивая результаты выполнения двух пунктов приходи к выводу, что для каждого закона распределения вероятностей имеется свой оптимальный алгоритм поиска либо последовательный, либо дихотомический, либо комбинированный алгоритм поиска.

3. Разработка оптимального алгоритма поиска экспоненциального закона распределения при числе измерений от N=15 до N=log2M

Для экспоненциального распределения вероятностей из пункта 2 последовательно уменьшая максимальное число измерений от до , разработайте оптимальные алгоритмы поиска и по результатам моделирования определите соответствующие значения среднего числа измерений .

При N=15 из предыдущего пункта оптимальным является последовательный алгоритм поиска и для него значение среднее значение двоичных измерений определяется так же как и для потенциальной скрытности. Значение Rcpпредставлено в таблице 1.

Таблица 1 – Зависимость среднего числа измерений

от числа измерений при оптимальных алгоритмах поиска

ТN	33	44	55	66	77	88	99	110	111	112	113	114	115
КRср	ннельзя	4	22.875	22.4062	22. 2011	22.0956	22.0343	.2.0077	22.0038	22.0013	12.0003	11,9998	11.9997

Далее при N=14.

Проведем расчет потенциальной скрытности для каждого случая по формуле 1:

При числе измерений равному 3-м, разработать алгоритм поиска невозможно, так это не удовлетворяет условию реализуемости поиска, а именно:

(2)

В результате построен график зависимости среднего числа измерений от числа измерений представленный на рисунке 8.

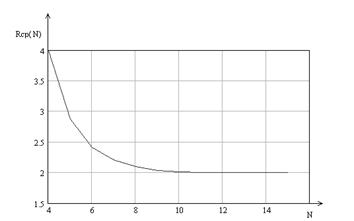
Рисунок 8 – Зависимость среднего числа измерений от числа измерений для экспоненциального закона распределения вероятности

4. Разработка оптимального алгоритма поиска для 9-го варианта распределения при числе измерений от N=1 до 15

Для своего варианта распределения вероятностей при числе событий разработайте оптимальный алгоритм поиска, постройте дерево поиска, объясните его форму, чем она обусловлена?

На наборном поле задайте оптимальный полный алгоритм поиска. Последовательно исключая последние измерения (до ), рассмотрите зависимость среднего числа измерений , вероятности неполного решения и остаточной скрытности от продолжительности поиска . Результаты представлены в таблице 2.

Таблица 2 – Зависимость среднего числа измерений,

остаточной скрытности, вероятности неопределенности от числа измерений

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
R	4	3.775	4.325	4.725	5.1625	5.375	5.5	5.65	5.7	5.7625	5.8	5.8
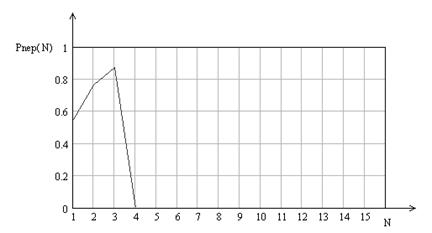
Pнеоп	0.55	0.7625	0.875	0	0	0	0	0	0	0	0	0	0	0	0
Sост	0.801	0.785	0.791	0.802	0.814	0.826	0.837	0.848	0.858	0.868	0.877	0.885	0.893	0.901

В данной таблице Sост считалось при доверительной вероятности 0.9. «PrintScreen» программы «Poisk» при различных значениях числа измерений представлен на рисунках 8-11.

При числе измерений меньше 4-х появляется вероятность неполного решения, связанная с тем, что невозможно проверить все события. В результате приходится проверять не все, оптимальным вариантом будет проверка наиболее вероятных событий. «PrintScreen» программы «Poisk» при числе измерения меньше 3-х представлена на рисунке 12.

Построим график зависимости потенциальной скрытности от числа измерения, который представлен на рисунке 13.

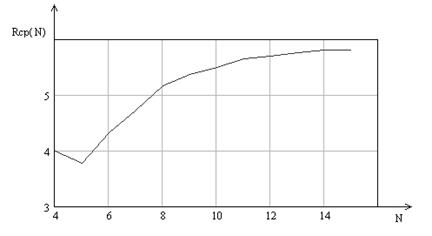
Рисунок 13 – Зависимость среднего числа измерений от числа измерений для 9-го закона распределения вероятности