Курсовая работа: Оптимизация режимов резания на фрезерном станке
Находим обратную матрицу:
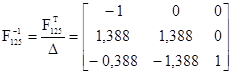
Находим решение исходного базиса:
;
.
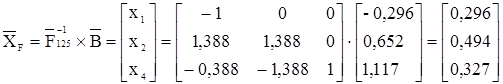Базисное решение является допустимым, т.к все его значения положительные.
Вычислим симплекс-разности для всех переменных, не вошедших в базис:
;
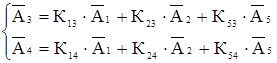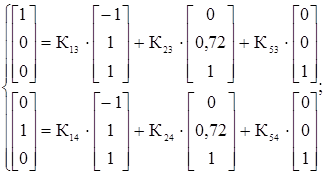
Симплекс разности отрицательны, следовательно, найдено оптимальное решение: 
Вывод: результаты, полученные графическим и симплекс-методом совпали, значит задача решена правильно.
3. Симплекс-таблицы. Решить систему уравнений:
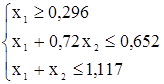
Найти значения, при которых целевая функция
.
Приведем все знаки к одному направлению:
Для перехода от системы неравенств, вводим в систему уравнений единичную матрицу. Расширенная форма записи:
; 
.
Приведем систему уравнений к виду, где выделены базисные переменные:
По последней записи системы уравнений и целевой функции построим таблицу 1.
После нахождения разрешающего элемента в таблице 1, переходим к заполнению таблицы 2. После построения таблицы 2 в последней строке имеется положительный элемент, значит оптимальное решение не найдено.
Определяем разрешающий элемент в таблице 2 и переходим к заполнению таблицы 3.
Таблица 3.
| Таблица 1 | Таблица 2 | Таблица 3 | |||||||||
|
СН БН | СЧ | х1 | х2 |
СН К-во Просмотров: 283
Бесплатно скачать Курсовая работа: Оптимизация режимов резания на фрезерном станке
| |||||||