Курсовая работа: Организация обобщающего повторения на уроках геометрии в 7 классе

Последний вопрос приводит к следующим двум задачам:

1. Доказать, что треугольники ABC и A ₁ B ₁ C ₁ равны, если АВ =А₁ В₁ , BC =B ₁ C ₁ и углы A и A ₁ равны.

2. Доказать, что треугольники АВС и А₁ В₁ C ₁ равны, если углы A и A ₁ , B и B ₁ , C и С₁ равны (задача №174 из учебника).

4) Решение задач (письменно).

В классе учащиеся решают задачу 1; задача 2 задается на дом (т.к. при ее решении используется теорема о сумме углов треугольника, которую учащиеся должны будут повторить к следующему уроку).

Решение задачи 1

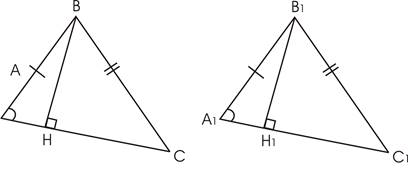
Дано: АВ =А₁ В₁

BC =B ₁ C ₁ и углы A и A ₁ равны.

Доказать: ∆ABC =∆A ₁ B ₁ C ₁

Доказательство:

Дополнительные построения: BH ┴ AC , B ₁ H ₁ ┴ A ₁ C ₁

1) Рассмотрим прямоугольные треугольники ABH и A ₁ B ₁ H ₁

По условию AB =A ₁ B ₁ , углы А и А₁ равны => ∆ABH =∆A ₁ B ₁ H ₁ , (по гипотенузе и острому углу) => AH =A ₁ H ₁ , BH =B ₁ H ₁ .

2) Рассмотрим прямоугольные треугольники ∆CBH и ∆C ₁ B ₁ H ₁ .

По условию BC =B ₁ C ₁ ,по доказанному BH =B ₁ H ₁ => ∆CBH =∆C ₁ B ₁ H ₁ (по гипотенузе и катету) =>CH =C ₁ H ₁ .

3) По доказанному AH =A ₁ H ₁ , CH =C ₁ H ₁ => AC =A ₁ C ₁ .

4) Рассмотрим треугольники ∆АВС и ∆A ₁ B ₁ C ₁ .

По условию AB = A ₁ B ₁ , BC =B ₁ C ₁ , по доказанному AC =A ₁ C ₁ => ∆ABC =∆A ₁ B ₁ C ₁ (по III признаку), что и требовалось доказать.

Если остается время, то учащиеся решают задачу №175 из учебника.

175.

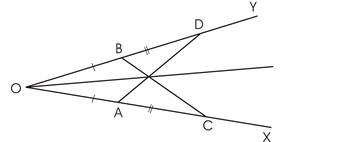Дано: ОА=ОВ, АС=ВВ .

Доказать: ОЕ – биссектриса.

Доказательство:

1) По условию ОА=ОВ, АС=ВО => ОС=ОО .

2) Рассмотрим треугольники ∆АО D и ∆ВОС .

По условию ОА =ОВ , по доказанному ОС =О D , угол COD – общий => ∆АО D и ∆ВОС (по I признаку) => углы OAD и OBC равны, углы ODA и OCB тоже равны.

3) По доказанному углы OAD и OBC равны => углы EAC и EBD тоже равны.

4) Рассмотрим треугольники ∆АЕС и ∆ВЕС .

По условию АС =ВВ , по доказанному углы ЕАС и ЕВВ равны, углы АСЕ и ВВЕ равны => ∆АЕС =∆ВЕ D (по II признаку) => АЕ =ВЕ .

5) Рассмотрим треугольники ∆ОАЕ и ∆ОВЕ .