Курсовая работа: Основи теорії графів. Властивості ойлерових та гамільтонових графів

Теорема 1.4. Число усіх орієнтованих графів з вершинами дорівнює .

Доведення . Справді , число впорядкованих пар елементів з дорівнює , тому число всіх можливих множин дуг дорівнює .

Означення 1.13.

Нехай -множина вершин. Орієнтованим графом з петлями будемо називати пару множин , де (див.рис.1.20).

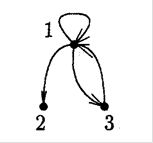
Рис.1.20. Орієнтований граф з петлями в якому ,

Теорема 1.5. Число орієнтованих графів з петлями , які мають вершин, дорівнює .

Доведення. Справді, число різних множин (підмножин множини ) дорівнює .

Якщо розглядається одночасно декілька типів графів, то графи які описуються означення (1.1), будемо називати простими графами.

Якщо в означенні (1.1) до множини невпорядкованих пар приєднати ще множину всіх пар виду , то відповідний граф називається простим графом з петлями.

З теореми 1.5 випливає довід теореми 1.6 про прості графи.

Теорема 6. Число всіх простих графів з вершинами і петлями дорівнює

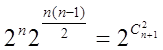
Надалі, ми будемо розглядати прості графи.

РОЗДІЛ ІІ ОЙЛЕРОВІ ГРАФИ

2.1 Ойлерова ломиголовка «Кенігзберзьких мостів»

Для рішення серйозних математичних задач математик Ойлер(Euler) використовував наочні ломиголовки. Одна з них поклала початок зовсім новій області досліджень, що виросла згодом у самостійний розділ математики - теорію графів і топологію. Особливість цієї теорії - у геометричному підході до вивчення об'єктів.

Теорія графів – одна з небагатьох математичних дисциплін, дата народження якої може бути встановлена абсолютно точно.

Перша робота з теорії графів належить Леонарду Ойлеру. Вона з’явилась в публикаціях Санкт-Петербургзської Академії наук у 1736 році.

Праця Ойлера розпочиналася з розгляду однієї ломиголовки так званої „задачі про кенігзберзькі мости”

Місто Кенігзберг (нині Калінінград) розташоване на берегах річки Прегель і двох островах. Різні частини міста сполучені сімома мостами. Щонеділі жителі міста любили здійснювати прогулянки по місту. Ойлер поставив питання: чи можна здійснити прогулянку, вийшовши з дому і повернувшись до нього , таку , щоб по кожному мосту пройти рівно один раз.

Сформулюємо задачу, як задачу теорії графів. Схематична карта міста зображена на рисунку 2.1..

Рис. 2.1. Схема мостів в Кенігзберзі [11]

Чотири частини міста зображені літерами Оскільки нас цікав-лять лише переходи через мости, ми можемо вважати вершинами графа, ребра якого відповідають мостам. Цей граф зображено на рисунку 2.2.

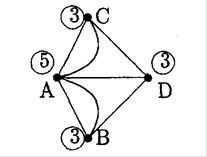
Рис. 2.2. Граф «Кенігзберзьких мостів» в ломи головці Ойлера

Ойлер зауважив, що цей граф не являє єдиного циклу; з якої б вершини ми не почали б обхід , ми не можемо обійти весь граф і повернутись назад, не проходячи жодного ребра двічі. Якби такий цикл існував, то з кожної вершини виходило б стільки ребер , скільки в неї входить , інакше кажучи степінь кожної вершини була б парним числом. Таким чином, відповідь на питання Ойлера-негативна.

Виклавши розв язання задачі про кенігзберзькі мости , Ойлер в своїй праці поставив питання : на яких графах можна знайти цикл, який містить всі ребра графа, при чому кожне ребро зустрічається в циклі рівно один раз?

Це дало початок системному математичному підходу до побудови та вивчення властивості графів.

2.2 Основні поняття та означення ойлерових графів

Означення 2.1

Зв’ яний граф називається ойлеровим графом, якщо існує замкнений ланцюг, який проходить через кожне ребро.Такий ланцюг будемо називати ойлеровим ланцюгом, або ойлеровим циклом (див.рис.2.3)

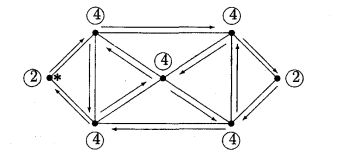
Рис.2.3. Структура вершин та ребер в неорієнтованому ойлеровому графі (* - означено точку входу ойлерового ланцюга - циклу)