Курсовая работа: Основи теорії графів. Властивості ойлерових та гамільтонових графів

Граф називається напівойлеровим, якщо існує ланцюг , який проходить через кожне його ребро рівно один раз (див рис.2.4).

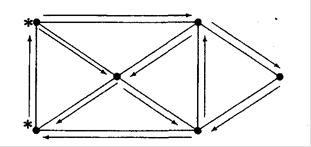
Рис.2.4. Структура вершин та ребер в неорієнтованому напівойлеровому графі (* - означено точку початку та кінця ойлерового ланцюгу)

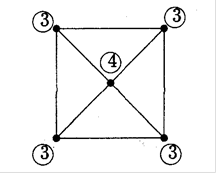
Рис.2.5. Приклад неойлерового графу

Дослідивши структуру неойлерового графу, наведеного на рис.2.5, розг-лянемо необхідні і достатні умови для того, щоб граф був ойлеровим. Доведемо лему, яка далі буде грати істотну роль.

Лема 2.1

Якщо степінь кожної вершини графа не менше двох , то граф містить цикл.

Доведення. Якщо в графі є петлі або кратні дуги, то твердження леми оче-видне. Тому надалі будемо припускати , що є простим графом. Нехай – довільна вершина графа . Побудуємо по індукції маршрут

обираючи вершину , суміжну з , а при обираючи вершину , суміж-ну з і відмінну від (існування такої вершини випливає з умови леми). Оскільки має скінченне число вершин, то врешті-решт ми прийдемо до вершини , з якої вийшли. Отримаємо цикл

Лема доведена.

Теорема 2.1 Для зв’язного графа наступні умови еквівалентні:

1. - ойлерів граф;

2. кожна вершина має парний степінь;

3. множину ребер графа можна розбити на прості цикли.

Доведення.

Нехай - ойлерів цикл графа . Будемо рухатись по циклу . Проходження кожної вершини збільшує степінь кожної вершини на 2, і оскільки кожне ребро входить в рівно раз , то будь-яка вершина має парний степінь .

Оскільки - зв’язний граф , степінь кожної вершини дорівнює принаймні 2; тому в силу леми 2.1 містить простий цикл . Виключимо ребра циклу , отримаємо остовний підграф , в якому кожна вершина має парний степінь. Якщо немає ребер , то (3) доведено. В протилеж-ному випадку застосуємо проведені вище міркування до , отримаємо граф , в якому степені всіх вершин є парними і так далі. Одночасно з порожнім графом , отримаємо розбиття множини ребер на циклів

Нехай множину ребер можна розбити на прості цикли. Нехай – один з простих циклів. Якщо складається тільки з цього циклу , то -ойлерів граф. В протилежному випадку існує інший простий цикл, який має вершину , спільну з . Ланцюг, який розпочинається з і складається з циклу і наступного за ним циклу , є замкненим ланцюгом, який містить всі ребра графа , кожне один раз . Отже , - ойлерів граф.

З теореми 2.1 випливає наступна теорема.

Теорема 2.2. Зв’язний граф є ойлеровим тоді і тільки тоді, коли кожна його вершина має парний степінь.

.

Рис.2.6. Приклад ойлерового графу в теоремі 2.2

Доведення. Граф зображений на рисунку 2.6. є ойлеровим, оскільки

1. Степінь вершин А, F, D, C, Q= 4(парні);

2. Степінь вершин B, E = 2(парні);

3. Множина ребер цього графа є об’ єднання двох простих циклів

і .