Курсовая работа: Основы программирования
![]()
Где j-n-2, n-3,…,0
Начертим блок-схему для функции обратной подстановки


Начертим блок-схему для функции определения наибольшего коэффициента ![]() и перестановки уравнений при необходимости.
и перестановки уравнений при необходимости.

Аппроксимация функций методом наименьших квадратов
Пусть в результате эксперимента получается следующая таблица значений:
| x0 | x1 | … | xn-1 |
| y0 | y1 | … | yn-1 |
Требуется найти аналитический вид функции, которая в точках x0 , x1 ,…,xn -1 будет иметь значения достаточно близкие к y0 , y1 ,…,yn -1.
Рассмотрим наиболее простой вид аппроксимации, т.е. замены таблицы значений аналитическим видом функции – аппроксимацию линейной функцией, т.е. будем находить функцию y=a0 *x+a1 , из которой в точках x0 , x1 ,…,xn -1 значения будут близки к y0 , y1 ,...,yn -1 . В качестве критерия близости будем рассматривать квадратичный критерий качества
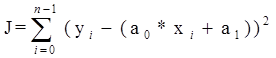 (1)
(1)
Необходимо найти коэффициенты a0 и a1 , чтобы критерий качества стремился к минимуму. Как известно, необходимое условие минимума – равенство 0 первых производных функции по соответствующим переменным. Найдем производные критерия качества (1) по переменным a0 и a1
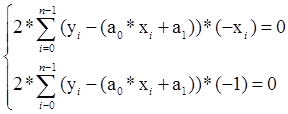 (2)
(2)
Разделим каждое из уравнений системы (2) на -2 и поставим неизвестные перед коэффициентами
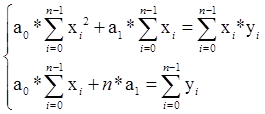 (3)
(3)
Система (3) – система из двух линейных уравнений с двумя неизвестными. Будем решать его методом алгебраического сложения. Первое уравнение системы (3) умножим на n, а второе уравнение на ![]() и вычтем из первого уравнения второе, из второго уравнения системы (3) получим выражение для a1
и вычтем из первого уравнения второе, из второго уравнения системы (3) получим выражение для a1
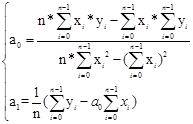
![]()
Аппроксимация квадратичной функции:
Пусть дана таблица значений
| x0 | x1 | ……… | xn-1 |
| y0 | y1 | ……… | yn-1 |
Требуется аппроксимировать эту таблицу полиномом третьего порядка, т.е. требуется найти коэффициенты полинома y=a0 x2 +a1 x+a2 , который в точках x0 , x1 , … , xn -1 имеет значения достаточно близкие к y0 , y1 , … , yn -1 .
В качестве критерия близости выберем квадратичный критерий качества, который должен стремиться к минимуму.
=![]() (1)
(1)
Найдем производные функции (1) по переменным а0 , а1 и а2 .
2*![]()
(2) 2*![]()
2*![]()
Разделим каждое уравнение системы (2) на (-2) и поставим коэффициенты после неизвестных