Курсовая работа: Оценка качества фотоаппаратов
1)Найдем по формуле (1) (п.3) W(1) по следующему алгоритму:
1. Умножим исходную матрицу на вектор e, получим вектор;
2. Умножим полученный вектор на вектор eT , получим число;
3.Разделим полученный вектор в пункте 1 на число, полученное в пункте 2, получим вектор, это и есть W(1).
Получили:
| W(1) |
| 0,35 |
| 0,09 |
| 0,38 |
| 0,18 |
По аналогичной схеме найдем W(2), вместо исходной матрицы используя ее квадрат.
Получили:
| W(2) |
| 0,44 |
| 0,10 |
| 0,34 |
| 0,13 |
2) Найдем модуль разницы W(1) и W(2) и получим следующий вектор:
| W(1)-W(2) |
| -0,09 |
| -0,01 |
| 0,04 |
| 0,05 |
Полученный вектор умножим на вектор eT , получим число, которое сравним с 0,001:
0,19>0,001 => повторяем алгоритм до тех пор, пока не найдем искомый вектор.
Число, меньшее 0,001 получили после 5-й итерации. Искомый вектор следующий:
| W(5) |
| 0,42 |
| 0,11 |
| 0,32 |
| 0,15 |
3) По аналогичному алгоритму была составлена матрица на основании мнения эксперта Б:
| I | II | III | IV | |
| I | 1,00 | 5,00 | 1,67 | 0,60 |
| II | 0,20 | 1,00 | 0,33 | 0,20 |
| III | 0,60 | 3,00 | 1,00 | 0,60 |
| IV | 1,67 | 1,67 | 1,67 | 1,00 |
Число, меньшее 0,001 получили после 3-й итерации:
| W(3) |
| 0,33 |
| 0,07 |
| 0,22 |
| 0,37 |
4) Для эксперта В исходная матрица:
| I | II | III | IV | |
| I | 1,00 | 1,67 | 5,00 | 1,67 |
| II | 0,60 | 1,00 | 1,67 | 1,67 |
| III | 0,20 | 0,60 | 1,00 | 0,33 |
| IV | 0,60 | 0,60 | 3,00 | 1,00 |
Число, меньшее 0,001 получили после 3-й итерации:
| W(3) |
| 0,42 |
| 0,26 |
| 0,10 |
| 0,23 |
3.2 Проверка согласованности экспертов
Для того чтобы определить согласованность между экспертами вычислим корреляцию между ними по формуле (3):
r=![]() , (3)
, (3)
где:
x и y — значения вектора приоритета для каждого эксперта.
Оказалось, что корреляция между А и Б равна 0,42; между А и В – 0,33; а между Б и В равна 0,26. Можно сделать вывод, что наиболее согласованны А и Б. Мнение эксперта В мы в дальнейшем учитывать не будем.
Найдем значение![]() (таблица 3.2.1):
(таблица 3.2.1):
Таблица 3.2.1
| W А | W Б | W ср | |
| I | 0,42 | 0,33 | 0,38 |
| II | 0,11 | 0,07 | 0,09 |
| III | 0,32 | 0,22 | 0,27 |
| IV | 0,15 | 0,37 | 0,26 |
Итак, получился вектор:
![]() (0,38; 0,09; 0,27; 0,26).
(0,38; 0,09; 0,27; 0,26).
4. Векторная оценка качества
Для того чтобы произвести векторную оценку качества необходимо найти длину вектора ║![]() ║.
║.
║![]() ║=
║=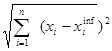 (4)
(4)
Найдем точку отсчета - Tinf ., точку с наихудшими показателями по всем объектам. Для этого воспользуемся таблицей 1 из пункта 1.2.
|
К-во Просмотров: 695
Бесплатно скачать Курсовая работа: Оценка качества фотоаппаратов
|