Площадь каждого прямоугольника

f_k Д= N_k /N = Р _k

есть вероятность попадания результата в интервал Д_k .. Сумма площадей прямоугольников, основания которых находятся внутри некоторого интервала [x ₁ ,x ₂ ], равна вероятности для каждого отдельного наугад взятого результата попасть в этот интервал.

Расчетная часть

В математической статистике исходная исследуемая случайная величина называется генеральной совокупностью, а полученный из нее набор экспериментальных данных – выборочной совокупностью, или выборкой.

1. Число объектов (наблюдений) в совокупности, генеральной или выборочной, называется ее объемом ; обозначается соответственно через Nи n. В данном случае N=100.

2. Числа n_i , показывающие сколько раз встречаются варианты x_i в ряде наблюдений, называются частотами , а отношение их к объему выборки – частостями p_i .

, (1)

где .

Проранжируем статистические данные. Для определения оптимального значения величины интервала в первом приближении можно воспользоваться формулой Стерджеса

(2)

Воспользовавшись (2) получим , .

В соответствии с (1) и (2) составим интервальный статический ряд:

Таблица 1

Итервальный статический ряд

Интервал	69,768-70,509	70,509-71,25	71,25-71,991	71,991-72,732	72,732-73,473	73,473-74,214	74,214-74,955	74,955-75,696	75,696-76,437
Частота	2	11	11	20	24	16	11	4	1
Частостьpi	0,02	0,11	0,11	0,2	0,24	0,16	0,11	0,04	0,01

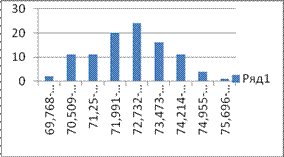
Рисунок 1. Диаграмма частоты в выбранных интервалах

3. Медианой вариационного ряда называется значение признака, приходящееся на середину ряда. В нашем случае имеем:

4. Размахом вариации называется число

,

где или – наибольший, – наименьший вариант ряда.

5. Выборочным средним называется среднее арифметическое всех значений выборки:

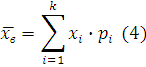
В случае интервального статистического ряда в качестве следует брать середины интервалов, а - соответствующие им частости.

6. Выборочной дисперсией D _в называется среднее арифметическое квадратов отклонений значений выборки от выборочной средней, т.е.

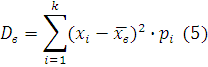
7. Выборочное среднеквадратическое отклонение выборки определяется формулой: