Курсовая работа: Оценка погрешностей измерений
8. Эмпирической (статистической) функцией распределения называется функция 
, определяющая для каждого значения x частость события 
: 
. Для нахождения эмпирической функции записывают в виде:
где n– объем выборке, nx – число наблюдений, меньших х . Согласно (7) определим значения эмпирической функции распределения в выбранных интервалах.
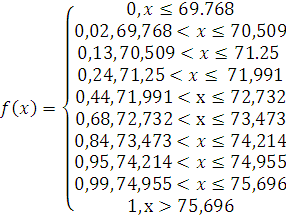
График эмпирической функции распределения имеет вид.
Одной из важных задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по эмпирическому распределению, представляющему вариационный ряд.
Проверим при уровне значимости 
гипотезу 
о том, что исследуемая выборка подчиняется нормальному закону распределения.
Рисунок 2. График эмпирической функции распределения
Число наблюдений в крайних интервалах меньше 5, поэтому объединим их с соседними. Получим следующий ряд распределения ( n=100).
| Интервалы | Частота k | Середина интервалаXcp |
| 69,768-71,25 | 13 | 70,694 |
| 71,25-71,991 | 11 | 71,62 |
| 71,991-72,732 | 20 | 72,362 |
| 72,732-73,473 | 24 | 73,102 |
| 73,473-74,214 | 16 | 73,844 |
| 74,214-74,955 | 11 | 74,584 |
| 74,955-76,437 | 5 | 75,377 |
Вычислим параметры, определяющие нормальный закон распределения.
Так как случайная величина имеет нормальное распределение, то для расчета вероятностей 
попадания случайной величины Xв интервал используем функцию Лапласа в соответствии со свойствами нормального распределения:
Полученные результаты приведем в следующей таблице:
| Xi , Xi+1 | 69,768-71,25 | 71,25-71,991 | 71,991-72,732 | 72,732-73,473 | 73,473-74,214 | 74,214-74,955 | 74,955-76,437 |
| ni | 13 | 11 | 20 | 24 | 16 | 11 | 5 |
| n`=n∙pi | 10,2 | 14,5 | 20,92 | 22,46 | 17,69 | 9,03 | 5,2 |
Определим критерий Пирсона:
Находим число степеней свободы. По выборке рассчитаны два параметра, значит 
. Количество интервалов 
. Следовательно, 
. Зная, что 
, по таблице находим 
. Поскольку 
считаем гипотезу верной.
9. Осуществим разбиение выборки на произвольное число интервалов, тем самым визуализировав вид плотности распределения случайной величины.
Таблица 2
Разбиение выборки на 20 и 30 интервалов
| № интервала | Интервал | Частота, ki | Интервал | Частота, ki |
| 1 | 70,138-70,327 | 1 | 70,138-70,422 | 2 |
| 2 | 70,327-70,516 | 1 | 70,422-70,705 | 4 |
| 3 | 70,516-70,705 | 4 | 70,705-70,988 | 2 |
| 4 | 70,705-70,893 | 1 | 70,988-71,271 | 6 |
| 5 | 70,836-71,082 | 2 | 71,271-71,554 | 3 |
| 6 | 71,082-71,271 | 5 | 71,554-71,837 | 5 |
| 7 | 71,271-71,459 | 2 | 71,837-72,120 | 4 |
| 8 | 71,,459-71,648 | 2 | 72,120-72,403 | 9 |
| 9 | 71,648-71,837 | 4 | 72,403-72,686 | 6 |
| 10 | 71,837-72,026 | 3 | 72,686-72,969 | 9 |
| 11 | 72,026-72,214 | 4 | 72,969-73,252 | 11 |
| 12 | 72,214-72,403 | 6 | 73,252-73,535 | 8 |
| 13 | 72,403-72,592 | 4 | 73,535-73,818 | 4 |
| 14 | 72,592-72,781 | 7 | 73,818-74,101 | 7 |
| 15 | 72,781-72,969 | 4 | 74,101-74,384 | 8 |
| 16 | 72,969-73,158 | 8 | 74,384-74,667 | 4 |
| 17 | 73,158-73,347 | 6 | 74,667-74,950 | 3 |
| 18 | 73,347-73,536 | 5 | 74,950-75,233 | 2 |
| 19 | 73,536-73,725 | 4 | 75,233-75,517 | 1 |
| 20 | 73,725-73,913 | 3 | 75,517-75,8 | 2 |
| 21 | 73,913-74,102 | 4 | ||
| 22 | 74,102-74,291 | 7 | ||
| 23 | 74,291-74,480 | 2 | ||
| 24 | 74,480-74,668 | 3 | ||
| 25 | 74,668-74,857 | 3 | ||
| 26 | 74,857-75,04 | 1 | ||
| 27 | 75,04-75,23 | 1 | ||
| 28 | 75,23-75,423 | 1 | ||
| 29 | 75,423-75,612 | 1 | ||
| 30 | 75,612-75,801 | 1 |
Рисунок 3. Диаграмма плотности распределения случайной величины с 20-и интервальным разбиением
Рисунок 4. Диаграмма плотности распределения случайной величины с 30-и интервальным разбиением
Рассчитаем основные параметры выборки для 20 интервалов:
