Курсовая работа: Передача дискретных сообщений

r- длина проверочной части кодовой комбинации;

Определим оптимальную длину кодовой комбинации n, обеспечивающую наибольшую относительную пропускную способность R и число проверочных разрядов r обеспечивающих заданную вероятность необнаруженной ошибки Рош при заданной кратности ошибок tоб внутри кодовой комбинации и заданной вероятности ошибок Рош в канале связи.

По результатам расчетов составляем таблицы для Рош = 0,0005 и Рош = 0,005:

L=5500 км; a=0.55; a0=4; V=80000 ; B=1200 Бод; Рно=3.0×10-6

n=2-1 ,где m=5...12

R = {1-3.32/n [(1-a)×lg n/d0-1+lg Pош - lg Pно]}× 1- Pош ×n (4+2LB/vn)

r = {3.32[(1-a)×lg n/dо-1+lg Pош - lg Pно]}

k=n-r

Таблица 1 Рош = 0,0005

R	n	r	k
0.69758	31	9	22
0.83337	63	10	53
0.90115	127	10	117
0,93277	255	11	244
0.94402	511	11	500
0.94254	1023	12	1011
0.93163	2047	12	2035
0.91202	4095	13	4082

nопт=511

Из таблицы 1 видно, что наибольшую пропускную способность R=0.94402 обеспечивает циклический код с параметрами n= 511, r= 11. k=500

Таблица 1 Рош = 0,005

R	n	r	k
0.47359	31	13	18
0.62827	63	13	50
0.6865	127	14	113
0,68048	255	14	241
0.62465	511	15	496
0.52192	1023	15	1008
0.36679	2047	15	2032
0.14655	4095	16	4079

nопт=127

Из таблицы 2 видно, что наибольшую пропускную способность R= 0,6865 обеспечивает циклический код с параметрами n= 127, r= 14 k=113.

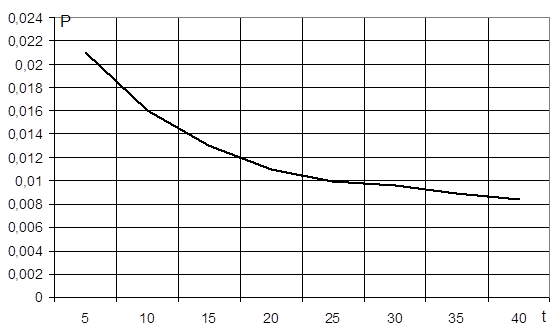Для полученой длинны блока построить граф розделения вероятности кратности ошибки.

Граф вероятностей P(t,n=n опт).

t£n/3

n=n оптимальный

n=511 P=0.0005

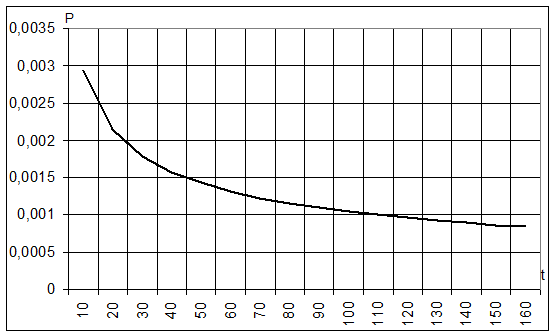n=127 P=0.005