Курсовая работа: Плаваючий потенціал електростатичного зонду в плазмовому гетерогенному середовищi

Від інших засобівплазменої діагностики зонди відрізняються тим, що дозволяють робити прямі локальні виміри параметрів плазми.

В даний час існує кілька основних напрямківплазмових досліджень [8], для кожного з яких значення і застосовність зондовихвимірів різні. У багатьох задачах газової електроніки здійснюються умови, у яких зондовівиміри зберігають домінуючу роль. Це справедливо в тому випадку, коли температура електронів і їхня концентрація не дуже великі, а магнітні поля малі. Теорія й експериментальна техніка зондових вимірів для плазми високої щільності в сильномумагнітному полі значно ускладнюється. У цьому випадку важко встановити правильний однозначний зв'язок між величиноюзондовогоструму і параметрами плазми. Слід зазначити збурений вплив зонда на плазму можна зменшити, направляючи останній у короткі проміжки часу з «гарячої» зони в областьрозташування зонда. Однак у цьому випадку на плазму збурену дію надають електромагнітні поля, за допомогою яких здійснюється такий добір. Нарешті, частинки гарячої плазми, що мають високі енергії, викликають вторинні процеси на поверхні зонда, що приводить до перекручування зондових характеристик.

Зонди застосовувалися для дослідження газових розрядів ще на початку минулого століття (наприклад, Круксом). Однак лише у 20-х роках Ленгмюр і його співробітники, розвивши теорію методу, зробили зондовий метод одним з найбільш ефективних засобівплазмової діагностики.

Дослідження Ленгмюра були обмежені випадком плазми низького тиску, колизіткненнями між частинками плазми можна знехтувати. У цьому випадку йому вдалося побудувати відносно просту і внутрішньо погоджену теорію. В даний час ясно, що деякі з припущень теорії Ленгмюра навряд чи виконуються при практичних додатках. Проте результати Ленгмюра і понині лежать в основі будь-якого дослідження, зв'язаногоз застосуванням зондів.

Суть методу полягала у вимірі струму заряджених частинок на малий заряджений електрод, поміщений у плазму. Залежність цього струму від потенціалу електрода називається зондовой характеристикою. З зондовой характеристики за певних умов можна обчислити основні параметри плазми — температуру і концентрацію заряджених частинок і потенціал простору. У деяких випадках зондовівиміри дозволяють визначити функцію розподілу частинок по енергіям.

Створюючи основи зондовой теорії, Ленгмюр виходив із припущення про рівноважну функцію розподілу заряджених частинок по швидкостях у збуреної плазмі. Він розглядав дві характерні зони: область плазми й область слоя поблизу зонда (або стінки).

Для наближеного визначення ходу потенціалу поблизу зонда були зроблені наступні припущення:

1) в області плазми можна знехтувати об'ємним зарядом частинок через її квазінейтральність;

2) в області слоя при негативному потенціалі зонда можна знехтувати зарядом, створюваним електронами;

3) утворення іонів в слої і вторинних частинок на поверхні зонда не відбувається;

4) на зовнішній границі слоя об'ємного заряду потенціал плазми звертається в нуль, тобто плазма за межами слоя не возмушена.

Виходячи з цих припущень легко знайти зв'язок між струмом зонда і параметрами плазми, що приводить до таких співвідношень для великого зонда(R₀ >>D) при не дуже високому негативному потенціалі:

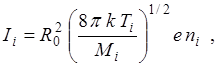(1.17)

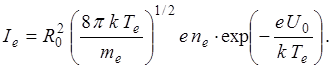(1.18)

Тут I_i і I_e — струми іонів і електронів на зонд відповідно; T_i і Ті — температури цих частинок; n_i і n_e — їх концентрації в невозмушеной плазмі; М_i і m_e -маса іона й електрона відповідно; U₀ і R₀ — потенціал і радіус зонда; D— дебаєвський радіус екранування; k — стала Больцмана; е — заряд електрона.

Зі співвідношення (1.18) видно, що по нахилі електронної характеристики в напівлогарифмічному масштабі легко визначити електронну температуру Ті. Іонний струм у випадку великого негативного зонда, по Ленгмюру, не залежить від його потенціалу (U<0). Для узгодження виразу (1.17) з експериментальними даними приходилосядопускати, що температура іонів у газовому розряді дуже велика. Це допущення не відповідало основним теоретичним представленням і даним інших експериментальних методів вимірів.

У роботах Ленгмюра фактично не було враховане проникнення електричного поля зонда в квазінейтральну плазму, у зв'язку з чим величина потоку частинок, що притягаються, виявилася заниженою.

Згодом Бомом був отриман вираз для іонного струму з урахуванням проникнення поля зонда в плазму. Зневажаючи тепловим рухом частинок, що притягаються, Бомодержав для випадкуTe>>Ti досить важливе наближенеспіввідношення, що широко застосовується при обробці результатів зондових вимірів

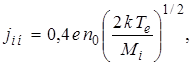(1.19)

де — густина іонного струму насичення. Відповідно до цього співвідношення, потік іонів на зонд залежить лише від температури електронів і практично не залежить від теплового руху іонів у невозмушеной плазмі.

Найважливішими факторами, щовизначаютьвидзондової характеристики, є середня довжина вільного пробігу заряджених частинок і напруженість магнітного поля в зоні виміру. У зондовій теорії при відсутності магнітного поля розглядають такі співвідношення між довжиною вільного пробігу і розміром зонда:

У першому випадку зіткнення між частинками відіграють незначну роль; у третьому — варто враховувати зіткнення і дифузійні процеси в газі. Другий випадок є проміжним. Магнітне поле викривляє траєкторії частинок і тим самим впливає на величинузондовогоструму. Колиларморовський радіус обертання заряджених частинок стає порівняннимабо менше розмірів зонда, важливу роль починають грати дифузійні процеси в магнітному полі.

Надалі теорія зондових вимірів розвивалася в роботах Венцеля, Аллена, Бойда і Рейнольдса, Бернштейна і Рабиновича, Кагана і Переля й інших авторів. У деяких з цих робіт задачу про розподіл потенціалу вирішували чисельно у всій збуреній області поблизу зонда. Цей метод рішення більш точний у порівнянні зі штучним прийомом поділу збуреної зони на області слоя і плазми, що спрощує обчислення.

1.4. Конструкція зондів.

Матеріал колекторної частини зонда повинний бути стійкий стосовно розпиленню, нагріванню і хімічним реакціям [8]. Крім того, робота виходу матеріалу зонда повинна бути досить високою, щоб звести до мінімуму вторинні процеси. До числа таких процесів відносяться електронна емісія під дією бомбардування іонами або метастабільними атомами, фотоефект і термоелектронна емісія. Тому у випадку гарячих і щільних плазм широко використовуються молібден, вольфрам і тантал. У холодних же плазмах низької щільності можливо також використання нікелю, нержавіючої сталі і платини. У таблиці перераховані деякі важливі властивості матеріалів для зондів.

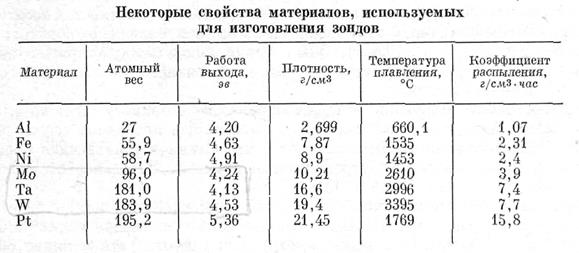
Вибір матеріалу для ізоляції держателя зонда визначається головним чином температурою плазми. Ізоляційні матеріали варіюються від простого скла або кварцу у випадку холодних плазм до спеціальних керамічних матеріалів, таких, як спеченний окис алюмінію і різні сполуки магнію, кремнію і цирконію у випадку гарячих плазм.

2. Потенціал електростатичного зонду в плазмовому гетерогенному середовищі.

Зазвичай лінійні розміри зондів, що використовуються для діагностики запиленої плазми лежать в інтервалі [0.1, 10.0] мм та помітно перевищують як дебаєвську довжину електронного компоненту запиленої плазми, так і лінійний розмір конденсованих частинок, що їх ансамбль утворює пиловий компонент запиленої плазми. Так наприклад для плазми продуктів згоряння алюмінізованих пальних [9] параметри гетерогенних плазмових систем лежать в області, де температура Т~2000 K, розмір макрочастинок конденсованої дисперсної фази см, середньооб’ємна концентація електронного компоненту м^-3 . Отже дебаєвська довжина електронів буде

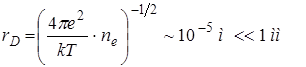(2.1)

В розріджених системах, наприклад космічній запиленій плазмі [1,10], ця нерівність може бути протилежною. Тому зосереджуємо увагу на головному: дослідженні зарядової рівноваги і стабільності зонду, що контактує з гетерогенною плазмовою середою. Будемо розглядати у подальшому модель необмеженої запиленої плазми, яку утворюють електрони, іони та заряджені частинки конденсованої дисперсної фази і яка перебуває в динамічній рівновазі (щодо обміну електронами) з пасивним сферичним металевим зондом радіуса R. Такі характеристики речовини зонду, як енергія Фермі електронів провідності , діелектрична проникність та робота виходу металу зонду будемо вважати відомими для заданої температури плазми T . Крім того, внесення пасивного зонду в необмежену гетерогенну плазмову середу ніяк не може вплинути на її характеристики “на нескінченості”: рівноважну концентрацію електронів запиленої плазми n_e , їх електрохімічний потенціал F, середній заряд індивідуальних макрочастинок конденсованої дисперсної фази у плазмі.

Таким чином, у загальному випадку, визначення електрофізичних характеристик зонду (заряду та потенціалу, а також розподілу локального максвелівського електростатичного поля в його околі) буде зводитись до вирішення проблеми зарядової рівноваги індивідуальної сферичної макрочастинки в гетерогенному плазмовому середовищі – запиленій плазмі.

Згідно з принципом детальної рівноваги [11] в термодинамічній рівновазі, кожен канал зміни зарядового стану зонду: емісія та прилипання газових електронів до зонду; іонізація та рекомбінація атомів та молекул на його поверхні; перерозподіл заряду між зондом та макрочастинками КДФ - є збалансованим дією протилежного йому каналу, і, загалом, у часі пасивний зонд зберігає з точністю до флуктуацій свій статистично середній заряд (z - зарядове число, е - модуль елементарного заряда) [12]. Отже, в статистичній рівновазі співвідношення, що виражає факт балансу потоків електронів емісії та прилипання на поверхні зонду, може бути обраним у якості основного рівняння для опису його зарядової рівноваги з оточуючою запиленою плазмою. Пов’язавши з центром зонду систему координат Лагранжа та здійснюючи в ній статистичне осереднення миттєвого електростатичного потенціалу, що його визначено миттєвими конфігураціями зарядів у плазмі, отримаємо завдання про розподіл самоузгодженого електростатичного потенціалу та об’ємного заряду в околі та всередині зонду. Оскільки рівноважні параметри запиленої плазми покладаються відомими, то при вирішенні проблеми основний акцент зосередимо на вирішенні “внутрішньої задачі’ про розподіл самоузгодженого потенціалу та заряду у власному об’ємі зонду. Тоді рівняння Пуасона-Фермі для перенормованого за допомогою енергії Фермі речовини зонда самоузгодженого електростатичного потенціалу 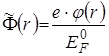у сферичній, пов’язаній з центром зонду системі координат запишемо як

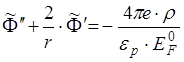(2.2)

Тут - густина об’ємного заряду в області зайнятій зондом, у наближенні Томаса-Фермі для електронів провідності металу визначається як

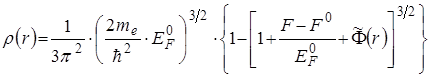(2.3)

де – маса електрона; постійна Планка; F – електрохімічний потенціал електронів запиленої плазми; електрохімічний потенціал матеріалу зонда ( ).

Враховуючи симетрію завдання та збереження зондом у рівновазі із запиленою плазмою деякого усталеного (осередненого за часом) розподілу внутрішнього самоузгодженого електростатичного потенціалу , доповнимо рівняння Пуасона-Фермі (2.2) граничними умовами у центрі

; (2.4)