Курсовая работа: Плоские задачи теории фильтрации
Трещиноватые коллекторы подразделяются на:
1) коллекторы смешанного типа, для которых емкостью служат трещины, каверны, микрокарсты, стилолиты, поровые пространства; ведущая роль в фильтрации нефти и газа принадлежит развитой системе микротрещин, сообщающих эти пустоты между собой;
2) чисто трещинного типа — емкостью служат трещины и по ним же осуществляется фильтрация.
Коллекторы смешанного типа в свою очередь подразделяются на подклассы: трещиновато-пористые, трещиновато-каверновые, трещиновато-пористо-каверновые коллекторы и т. д. Каждый такой подкласс определяется тем, какие категории пустот являются главными вместилищами для нефти (газа). Так, в трещиновато-пористом коллекторе основные запасы нефти (газа) содержатся в порах, а фильтрация осуществляется по развитой системе микротрещин. В дальнейшем мы подробно рассмотрим условия фильтрации в трещиновато-пористых коллекторах и коллекторах чисто трещинного типа.
????? ?? ????????? ??????????, ??????????????? ???????????? ?????????, ???????? ?????????????? т (??????????? ??????????????, ?????????? ?????? ? ?????????? ????????? ???????????). ??????????????? ?????????? ????????? ?????? ?????? ??????? t? ?? ????? ?????? ??????? t ???????????? ?????:
Выражается эта величина обычно в процентах. Трещиновато-пористые коллекторы имеют два типа естественных пустот:
а) межзерновая (первичная) пористость, аналогичная пористости для обычных песков, песчаников;
б) вторичная пористость (трещиноватость), обусловленная развитием трещиноватости, появившейся за счет различных причин. Пустоты этого типа имеют большие раскрытия, чем обычные раскрытия пор, и в значительной степени обусловливают фильтрационные свойства коллектора.
В соответствии со сказанным такие коллекторы рассматриваются Г. И. Баренблаттом, Ю. П. Желтовым и И. Н. Кочиной как совокупность двух разномасштабных пористых сред (рис.1)- системы трещин (среда 1), где пористые блоки играют роль «зерен», а трещины — роль извилистых «пор», и системы пористых блоков (среда 2).
Для трещиновато-пористого коллектора помимо коэффициента трещиноватости то, следует еще ввести коэффициент пористости тип» характеризующий среду 2. Тогда общую (суммарную) пористость трещиновато-пористого коллектора можно получить, если к коэффициенту трещиноватости mT , прибавить коэффициент межзерновой пористости пористых блоков mn ..
Другим важным параметром трещиноватой среды является густота трещин.
Густота трещин есть отношение числа трещин n, секущих нормаль, к длине нормали, проведенной к поверхностям, образующим трещины.
??????? ?????? ????? ???????????, ???????? ??????? ?????. ???? ???????????? ????? ???????????? ????? ?????? ?????????????? ?????? ????????? ????????????? ? ??????????? ?????, ?????? ??? ??????? ????????? ???????? ? ????? ??????? ???? ?? ?????, ?? ??????? ?? ? ????? ??????, ???????????? ?? ??????? ???????? ??????
Тогда коэффициент трещиноватости
|
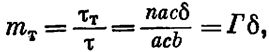 |
??? d ? ????????? ??????; ?, ? ? ??????????? ???????? ??????? ???????; b — ???????? (???. 2.1).
Как показали исследования ВНИГРИ, для трещиноватых пластов в большинстве случаев характерно наличие двух взаимно-перпендикулярных систем вертикальных трещин. Такая порода может быть представлена в виде модели коллектора, расчлененного двумя взаимно-перпендикулярными системами трещин с равными величинами раскрытия и густоты.
|
![]()
Для трех взаимно-перпендикулярных систем трещин, (рис. 2.2) с равными величинами раскрытия и густоты имеем:
|
В общем случае следует положить что:
|
где a — безразмерный коэффициент, зависящий от геометрии систем трещин в породе.
3.2 Проницаемость пласта.
|
??? ?? ????????? ?? ????????????? ??????? ?????????? ??? ??????? ???????? ??????? ???????? ????? ????? ???????? ???????????? ????????????? ????????:
|
?? ????????? (III.5), (III. 4) ????????? (II 1.6)-????????? ?????:
|
???????? ????????????? ??????????? ????????????? ??????, ??? ??? ??????? ?? (2.9)
???? ??????, ??? ? ??????? ?? ????????????? 1 ????? = 1,02?10-12 ?2 , ?? ??? ????????????? ??????
|
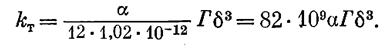 |
??? ???????????-????????? ?????? ????? ????????????? ???????????? ??? ????? ??????????? ? ???????????? ?????????????? ????????????? ??????, ????????????? ???? .
В продуктивных трещиноватых пластах горное давление, опре деляющее общее напряженное состояние среды, уравновешивается напряжениями в скелете породы и давлением жидкости в трещинах. При постоянстве горного давления снижение пластового давления за счет отбора жидкости из пласта приводит к увеличению нагрузки на скелет среды. С уменьшением пластового давления (давления жидкости в трещинах) уменьшаются усилия, сжимающие зерна (пористые блоки) трещиноватой породы. Значение этого фактора наряду со значительными силами инерции следует учитывать при исследовании процессов фильтрации в трещиноватом пласте. Таким образом, на объем пространства трещин в трещиноватом коллек торе влияют в основном два фактора:
1) увеличение объемов зерен с падением пластового давления;
2) увеличение сжимающих усилий на скелет продуктивного пласта.
Полагая, что в трещиноватом пласте преобладают упругие деформации и учитывая, что горное давление постоянно, а с изменением давления в жидкости, газе изменяются главным образом раскрытия трещин d, можно так оценить изменение раскрытия трещин от дав ления:
|
|
???????? ?????????? ? ???????????-???????? ??????? ????? ??????, ??? ? ??????????? ????? ?????????? ????, ????????????? ????. ?????? ????? ????????, ??? ? ???????????-???????? ?????? ??? ???????? ????????????? ??????? ????????????? ??????? ?????? (????? 1, ???. 2.1); ?????? ???????? ?????????? ???? ??????? ?????? ???? ??????? ???????? ??? ??????? ???????? ?????? (????? 2, ???. 2.1). ??????? ?????, ??? ??????????? ??? ????????????? ???? (2.13) ?? ????????????. ???, ??? ?????????? ?????????? ?????? ???????? ??????????????, ???????????? ??? ??????? ?????????? ???????? ? ??????? ??????? ???????????, ?????? (?. ?. ????????, ?. ?. ????????????) ?????????, ??? ?????????????, ?????????? (? ????? ???????? ? ????????? ????????????? ???????? ??? ????) ? ????? ???????? (????? 1 ? 2 ?? ???. 2.1) ????????
|
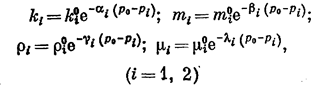 |
Некоторые авторы (А. Бан, И. Н. Николаевский, Н. П. Лебединец, Л. Г. Наказная) используют также линейную зависимость между трещинной проницаемостью и изменением давления в виде:
|
где a — реологическая постоянная трещиноватой среды, имеющая размерность, обратную размерности давления.
3.3 Границы применимости линейного закона фильтрации
Так же как и для гранулярных (пористых) сред, при больших скоростях фильтрации линейный закон фильтрации может нарушаться из-за появления значительных по величине сил инерции. Как показали исследования Г. М. Ломизе, для движения воды в щелях различного вида характерны числа Re, значительно превы шающие величины этого параметра для пористых сред: так, для щелей с гладкими стенками верхний предел применимости линейного закона оценивается числами Reкр = 600, а нижний —Reкр = 500).
Ф. И. Котяхов указывал, что для трещиноватых пород за счет изменения относительной шероховатости трещин и их различного раскрытия (от 71 мк до 12,96 мк в опытах Ф. И. Котяхова) нарушение линейного закона происходит при значенияхRe соответственно от 90 до 0,40. Исследования Е. С. Ромма подтвердили, что для щелей с гладкими стенками критическое число Рейнольдса равно 500. Им было также установлено, что если величина относительной шероховатости меньше 0,065, то ее роль в процессах фильтрации может не учитываться.
Параметр Re для трещиноватой среды можно ввести на основании следующих простых рассуждении.
|
??? u — ??????? ???????? ?????? ? ?/???; v ? ?????????????? ???????? ? ?/???; R — ?????????????? ?????? (????????? ??????? ???????? ??????? ?????? ? ???????????? ?????????) ? ?. ??? ?????? ?????????????? ???????:
|
??? а — ?????? ??????.
Приближенное выражение для R получено на основании того, что обычно d < а и величиной d в знаменателе по сравнению с а можно пренебречь. Заметим, что d — среднее раскрытие трещин в породе.
|