Курсовая работа: Плоские задачи теории фильтрации

(2.20)

?? ????????? ??? ????? ?????????? ? ???????????? ????????????? ????? ????? ???? ???????????? ? ????????????? ?????:
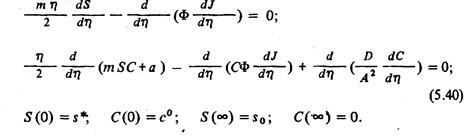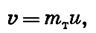
???????, ??? ???????? ??????????, ?? ?????? ??????? ????????? ????????? ?????? ?????????? ? ???????????? ?????? ??????? ??????? R?_др = 0,4. ???????, ??? ???? ???????? ????? ?????????? ?? ???????????? ??? ???????????? ???????, ??????? ???????????? ?????????? ??????.

(2.21)

???????????? ?????????? ?????? ?????????? ? ???? ??????????? ? ?????????? ??????. ??????????? ??????? ???????????? ????????? ??????:
??? п ?????????? ?? 1 ?? 1,75 (?? ?????? ????. ?. ?. ??????).

(2.22)

???????? ?????????? ?_т ????? ???????? ???????? ?????? ???????. ???????????? ????????????? ????????, ???:

(2.23)

???

где

(2.24)

?? ????????? (2.19) ????????? (2.18) ????? ???????? ? ????:

гдеn = 1 — 1,75.

При n = 1,75 имеем турбулентный режим. Если линейный закон нарушается, используется двучленная формула, учитывающая возрастающую роль сил инерции в связи с увеличением скоростей движения жидкостей и газов:

(2.25)

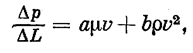
где a , b — некоторые постоянные.

Б. Ф. Степочкиным на основе обработки обширного эксперимен тального материала (по результатам опытных данных и заимствован ного из различных литературных источников) для большого диапа зона размеров (от нескольких микрон до 75 мм) твердых частиц раз нообразной формы (слагающих продуктивные пласты) и интервала чисел Re от 10^-6 до 10³ , получена двучленная формула:

(2.26)

??? d — ??????? ?????, ???????????? ?????

4. Расчетная часть

Капиллярная пропитка при физико-химическом и тепловом заводнениях. Нефтеотдача трещиновато-пористых коллекторов.

(3.1)

?????????? ??????, ??????? ???????? ???????????? ?????????? ???????????? ?????? ? ????????????? ???????? ???????????????? ??????? ???????? ????? ?????. ??????? ???????? ?????, ?????????? ???????????????? ?>0 ? ????????????? ??????????? ?????? ? ??????????? ?? ??? (???????????????? S?) ??? ??????????? ??, ?????????? ? ??????? ?? ????????? ?=0 ("?????") ? ?????? ????????? ??????????? ???????????? ?₀ , ??????????? ??? ??????????? T. ??? ????????? ??????????? ??? ? ??????? ????????? ?????????? ???????, ??????????? ???????????:

(3.2)

????? ????????? ???????? ???????? ? ????????????? ?????????? ??????????, ??? ???
? ?.?. ???????? ?????????????? ????????????, ??? ??? ? = const. ??? ???? ?? ??????? ?????????????? ???????? ??? ??¥ ("????? ?? ????? ???????") ???????, ??? ????????? ???????? ?????????? ???? ??? U=0. ????? ???????, ??????? ???? ??????????? ? ???????, ??????? ?? ????? ??????????? ?? ???? ????? ????? ? ????????, ??????????? ??? ????????????? ??????????? ????????.

Задача должна быть решена при условиях:

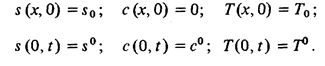
При этом особого комментария заслуживает величина s°- значение водонасыщенности в торцевом сечении образца. Это значение определяется условиями выхода нефти из образца. Действительно, вода вне образца и вода в той части образца, куда проникла пропитка, образуют единую связную фазу, и потому давление в ней при х =0 непрерывно:

(3.3)

? ⁼ ?? . ? ?????? ???????, ??????????? ????? ??????? ? ?????? ???? ? ???? ????????? ??????, ??????? ???????? ? ????? ??????? ? ???????? ???? ???? ?? ???????? ???????????? ????????, ??????????? ??????? ????????? ?????? r : ?₂ = ?_о + 2a/r . ???????????????? ???????? ??? ?????? ???????? ?????? ????? ???????

(3.4)

?????? ????? ?????????, ??? ??????? ????? ??????? ?? ????? ??????? ???, ? ??? ????????, ??? ???????????? s? ?????? ? ??????????? s*, ?????????? ????????? ? ???? ??????? ????????????? ??? ?????. ? ?????????? ??????? ??????????????

Учитывая условие U= О, имеем из уравнения

(3.5)

(3.6)

?????????? ?????? ? ????????????? ??????????? ???????? ????? ????????????? ??????? ????

удовлетворяющее системе обыкновенных дифференциальных уравнений

(3.7)

с условиями

Фактическое отыскание решения сформулированной задачи требует в общем случае привлечения численных методов. Для того чтобы выяснить некоторые важные общие свойства решений, рассмотрим два характерных частных случая.

(3.8)

?????????? ?????? ????? ??????????? ???????? ???????????? ????? ?????? ????????? ???????? ???????, ?? ??????????? ? ?????, (?=0), ? ?????????????? ????????. ????? ????? ???????, ??? ????????? ??????? ?????? ?? ????????????: a = а (с) . ??? ???? ????? ?????? ????? ?? ?????????, ? ??? ????????? ????????????? ??????? ????? ? ???????????? ????? ? ????????????? ?????????? ??????

??????? ?? ??????? ????????? ??????? ??????, ?????????? ?? ?, ???????? ??? ? ????

(3.9)

Характерное значение коэффициента капиллярного переноса А² значительно больше, чем характерное значение коэффициента диффузии D. Поэтому последний член в уравнении содержит множителем малый параметр D/A² < 1. Пренебрегая этим членом, получаем для С уравнение первого порядка

(3.10)

(3.11)

??????? ????? ????????? ??? ???????? ??????????? ????? ??? "?????????":

(3.12)

?????? ?????????? ????, ???????? ? "???????" ?? ??????? t,

Как и при "обычной" капиллярной пропитке, оно растет пропорционально корню из времени — факт, являющийся следствием автомодельности задачи.

(3.13)

?????? ?????????? ??????? ? ??????? ? ??? ?? ?????? ??????? ????? Qc = c?Qs. ? ?? ?? ?????

Как известно, скорость продвижения фронта капиллярной пропитки в зависимости от конкретных свойств функций фазовых проницаемостей и капиллярного давления может быть конечной или бесконечной. Примем здесь, что эта скорость конечна и существует выраженный фронт пропитки ns:

Равенство возможно только при n* < ns. Это означает, что при капиллярной пропитке гидрофильной среды, как и при закачке раствора активной примеси, фронт примеси отстает от фронта воды, а перед примесью движется чистая вода. Видно, что отставаниеобусловлено теми же двумя факторами, что и при закачке: адсорбцией

(а (с°) > 0) и смешением с погребенной водой (s_o > 0). Если Т - сред няя водонасыщенность в зоне, занятой примесью, то порядок величины отставания

(3.15)

Таким образом, из общих закономерностей процессов переноса следует, что примесь значительно отстает от "несущей" ее воды при капиллярной пропитке. Поэтому влияние ее на пропитку может ска заться лишь через посредство изменения гидродинамических харак теристик в области относительно больших водонасыщенностей.

Области больших водонасыщенностей отвечают малые значения ка пиллярного давления и сравнительно большие значения относительной фазовой проницаемости для воды. Поэтому существенное влияние на капиллярную пропитку примесь может оказывать лишь в том случае, когда она существенно изменяет вязкости фаз и относительную фазо вую проницаемость для нефти.

Второй существенный качественный результат получается из ана лиза первого уравнения системы (5.40). Обычным способом интег рирования по малому отрезку легко установить, что функция J непре рывна как функция nвсюду, в том числе и в окрестности точки n*, в которой концентрация примеси претерпевает разрыв согласно.

(3.16)

????? ???????, ??? n = n*?????

Поэтому если примесь изменяет кривую капиллярного давления (функцию Леверетта J), то скачок концентрации сопровождается скачком насыщенности такой величины, что капиллярное давление оказывается непрерывной функцией координат и времени.

Отмеченные выше особенности капиллярной пропитки гидрофильной пористой среды водным раствором активной примеси видны на рис. где показаны результаты модельных расчетов.

Обратимся теперь к другому важному частному случаю, а именно, рассмотрим процесс пропитки гидрофобной пористой среды раствором гидрофилизирующего ПАВ. Иными словами, предполагается, что пер воначально поверхность пор преимущественно смачивается нефтью (cosq < 0), однако поверхностно-активное вещество, растворенное в воде, способно, адсорбируясь на поверхности пор, превратить ее в гидрофильную (cosq > 0). Количественно эффект будет зависеть от величины адсорбции, а последняя, в свою очередь, в силу условия ло кального термодинамического равновесия, от концентрации ПАВ в воде. Поэтому далее принимается, что при некоторой пороговой концентра ции ПАВ с* происходит переход от гидрофобной среды к гидрофильной. Этот переход в гидродинамических уравнениях проявляется в изменении знака капиллярного давления рс: оно отрицательно для гидрофобной среды и положительно для гидрофильной, причем, как легко убедиться из простейших модельных рассуждении, производная ¶ p / ¶ s отрицательна как для гидрофильной, так и для гидрофобной среды.

Поэтому далее при модельных расчетах берется функция p_c (s, с) вида

(3.17)

Рассматривая изотермический случай, имеем вновь автомодельную задачу, описываемую первыми двумя уравнениями с соответст вующими краевыми условиями.

Удобнее, однако, рассмотреть эту задачу несколько по-иному. По скольку в гидрофобную среду водная фаза впитываться не может, ясно, что пропитка реально может происходить только в той части "образца", в которой концентрация ПАВ превысила критическое значение с*. Это означает, что ведущим в процессе пропитки должен быть процесс диффузии ПАВ, а пропитка должна следовать за ним. Возьмем поэтому в качестве автомодельной переменной

(3.18)

(3.19)

??? Do - ??????????? ???????? ???????????? ???????? ???????. ??? ???? ?????? ????????? ???????? ?

(3.20)

??-???????? ????????????? ???????????? ???????????? A² /Do > 1, ????????, ??? ? ???????? ??????? ??????????? ?????????
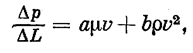
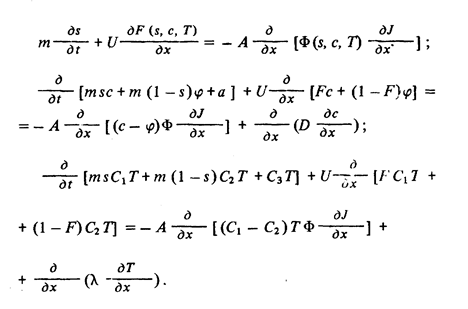
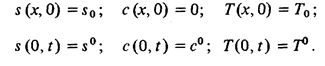
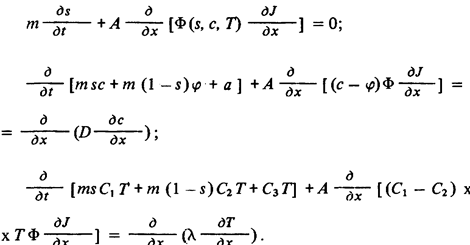
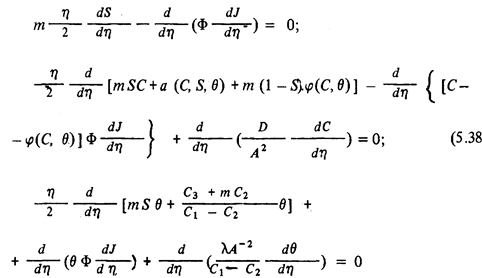
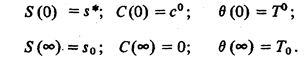