Курсовая работа: Поиск максимума одной функции многих переменных методом покоординатного спуска и с помощью метода

Перебирая всевозможные параметры p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума.

3. Решение задачи с использованием метода покоординатного спуска

3.1 Описание метода покоординатного спуска

Изложим этот метод на примере функции трех переменных .

Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; обозначим ее через . Найдем минимум функции одной переменной и обозначим его через . Мы сделали шаг из точки в точку по направлению, параллельному оси ; на этом шаге значение функции уменьшилось.

Затем из новой точки сделаем спуск по направлению, параллельному оси , т. е. рассмотрим , найдем ее минимум и обозначим его через . Второй шаг приводит нас в точку . Из этой точки делаем третий шаг – спуск параллельно оси и находим минимум функции . Приход в точку завершает цикл спусков .

Будем повторять циклы. На каждом спуске функция не возрастает, и при этом значения функции ограничены снизу ее значением в минимуме . Следовательно, итерации сходятся к некоторому пределу . Будет ли здесь иметь место равенство, т. е. сойдутся ли спуски к минимуму и как быстро?

Это зависит от функции и выбора нулевого приближения.

Метод спуска по координатам несложен и легко программируется на ЭВМ. Но сходится он медленно. Поэтому его используют в качестве первой попытки при нахождении минимума.

3.2 Алгоритм решения

Будем перебирать с с шагом какой-либо малой длины.

Зададим нулевое приближение, например:

Найдем частные производные .

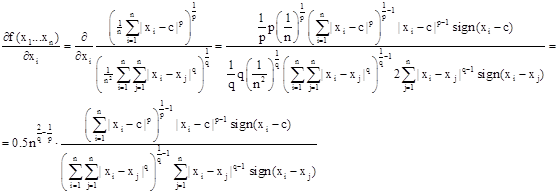
Пусть при каком-то j

Тогда k-ое приближение считаем по формулам:

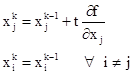
Шаг t будем выбирать таким образом, чтобы

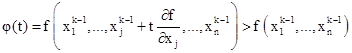и .

В результате, закончив процесс по критерию , где -заданная точность мы придем к набору, при котором функция f максимальна.

Подставим найденный набор и соответствующее в функцию f1=и перебрав все с, выберем те , при которых f1 минимальна.

Заключение

В ходе решения поставленной задачи рассмотрены случаи, когда n=4,5,6. Были найдены две основные области наборов :

1) x_i =0 или 1(количество 0 и 1 одинаково)

2) x_i =0.5, .

Причем участок 1<p<1.5 покрыт первой областью, при q>>p –– из первой области, при q≈p –– из второй области, а при p→∞ область делилась между ними примерно пополам.

На участке p>2 появлялись области вида:

i<k => x_i =0;

i>n-k => x_i =1;

k-1<i<n-k+1=> x_i =0.5.

На участке 2<q<3 p2 существует область, в которой максимум достигается при вида:

x_i =a => x_{n - i} =1-a, 0<a<1.

Список использованных источников