Курсовая работа: Показатели Ляпунова некоторой линейной стационарной системы

где− постоянны, совпадает с наибольшим из характеристических показателей комбинируемых решений, то есть имеем

Возьмем произвольную линейную комбинацию векторов

x и x.

Y=где −постоянны и (5).

Произведем арифметические действия над векторами x и x. Тогда равенство (5) примет вид

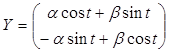(6).

Вычислим характеристический показатель линейной комбинации векторов (6).

Тогда по формуле (3) имеем

Итак, характеристический показатель линейной комбинации векторов совпадает с наибольшим из характеристических показателей комбинируемых решений x и x, значит, система векторов x и xобладает свойством несжимаемости (по определению4) Следовательно, фундаментальная система решений линейной стационарной системы (1) является нормальной фундаментальной системой (по теореме Ляпунова).

Найдем спектр системы (1).

Воспользуемся определением и следствием из теоремы Ляпунова.

Определение5 [1,c.137]. Спектром называется множество всех собственных характеристических показателей (то есть отличных от −∞ и +∞) решений дифференциальной системы.

Следствие [1,c.145]. Всякая нормальная фундаментальная система реализует весь спектр линейной системы.

Согласно определения5 и следствия из теоремы Ляпунова спектр стационарной системы (1) равен

Заключение

Таким образом, в процессе исследования линейной стационарной системы мы выяснили, что ее фундаментальная система решений является нормальной фундаментальной системой; нормальная фундаментальная система решений реализует весь спектр дифференциальной системы; спектр рассмотренной линейной стационарной системы равен.

Список использованной литературы

1. Б.П. Демидович "Лекции по математической теории устойчивости"-М.: Наука, 1967г., 465 c.

2. Н.М. Матвеев "Методы интегрирования обыкновенных дифференциальных уравнений"-М.: Высшая школа, 1967г., 564 с.