Курсовая работа: Порівняльний аналіз ефективності та складності прямих алгоритмів сортування масивів

Очевидно, що розглянутий алгоритм описує процес стійкого сортування. Загальна кількість операцій буде рівня (n-1 ), що відповідатиме при обрахунку кількості операцій O(n² ). Тому найгірший час сортування вставками дійсно є квадратичним.

2.2 Сортування бінарним включенням

Алгоритм прямого включення можна значно покращити, якщо врахувати, що "готова" послідовність є вже впорядкованою. Тому можна скористатися бінарним пошуком точки включення в "готову" послідовність. Тобто даний метод містить в собі метод бінарного пошуку елемента (пошук бінарним деревом) в масиві, в даному випадку – місця між елементами, де повинен бути розміщений даний елемент. Тому що пошук місця під наступний елемент можна зобразити як рух по дереву, від "стовбура" до "кореня". На першому кроці ділимо весь відсортований масив навпіл, далі порівнюємо даний елемент із елементами масиву з що посередині, якщо він менший, знову ділимо лівий підмасив, більший – правий. І так до тих пір поки не визначимо місце, де буде знаходитися даний елемент.

{l=1;r=j;tmp=mas[j];

while (l<r)

{

m=(r+l)/2;

if (mas[m]<=tmp) l=m+1; else r=m;

}

Нехай маємо впорядкований масив (8, 9, 10, 16, 18, 20, 35), покажемо жирним рух по бінарному дереву, для знаходження місця елементу = 19.

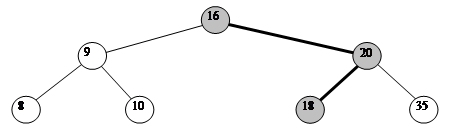
Програмна реалізація такого модифікованого методу включення матиме вигляд наступної програми (Файл SORT_2.СРР):

#include <conio.h>

#include <iostream.h>

#include <stdlib.h>

int mas[1000];

void vuv(int s)

{ for(int i=1;i<=s;i++)

cout<<mas[i]<<‘ ‘;

cout<<endl<<"--------------------------------"<<endl;

}

main()

{clrscr();

cout<<"Vvedit kilkist elementiv masuvy - n"<<endl;

int n,tmp,k;

cin>>n;

for (int i=1;i<=n;i++)

{

cout<<"vvedit "<<i<<" -element masuvy"<<endl;