Курсовая работа: Порівняльний аналіз ефективності та складності прямих алгоритмів сортування масивів

}

clrscr();

cout<<"Maemo masuv "<<endl;

vuv(n);

//Sort_binarn vstavkojy

int l,r,m;

for (int j=2;j<=n;j++)

{l=1;r=j;tmp=mas[j];

while (l<r)

{

m=(r+l)/2;

if (mas[m]<=tmp) l=m+1; else r=m;

}

for (i=j;i>=(r+1);i--) mas[i]=mas[i-1];

mas[r]=tmp;

}

cout<<"Masuv vidsortovanuy "<<endl;

vuv(n);

getch();

return 0;

}

Аналіз бінарного включення. Зрозуміло, що кількість порівнянь у такому алгоритмі фактично не залежить від початкового порядку елементів. Місце включення знайдено, якщо L=R . Отже вкінці пошуку інтервал повинен бути одиничної довжини. Таким чином ділення його пополам на i -ому етапі здійснюється log(i) раз. Тому кількість операцій порівняння буде:

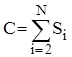, де , .

Апроксимуючи цю суму інтегралом, отримаємо наступну оцінку :

, де .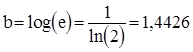

Однак істинна кількість порівнянь на кожному етапі може бути більшою ніж log(i) на 1 . Тому

.

Нажаль покращення, що породженні введенням бінарного пошуку, стосується лише кількості операцій порівняння, а не кількості потрібних переміщень елементів. Фактично кількість перестановок M залишається величиною порядку N² . Для досить швидких сучасних ЕОМ рух елемента, тобто самого ключа і зв’язаної з ним інформації, займає значно більше часу, ніж порівняння самих ключів. Крім того сортування розглядуваним методом вже впорядкованого масиву за рахунок log(i) операцій порівняння вимагатиме більше часу, ніж у випадку послідовного сортування з прямим включенням. Очевидно, що кращий результат дадуть алгоритми, де перестановка, нехай і на велику відстань, буде пов’язана лише з одним елементом, а не з переміщенням на одну позицію цілої групи.

2.3 Сортування прямим вибором