Курсовая работа: Построение эпюр поперечных сил, изгибающих моментов и выбор сечений балок
Рисунок 1
Задача 2
Построить эпюры Q и М для балки из дерева при q2 =5кН/м; P2 =10кН; M2 =35кНм (рис.2) и подобрать размеры балки прямоугольного поперечного сечения с отношением высоты к ширине h/b=3; ![]()
Решение
Для определения Q и М в любом сечении балки необходимо знать все внешние силы, действующие на балку, т. е. приложенные нагрузки и опорные реакции RA и RB .
Расположим начало координат в центре тяжести крайнего левого сечения, в точке А, ось Y направим вертикально вверх, а ось Х – горизонтально вправо (по оси балки).
На шарнирно-неподвижной опоре А неизвестную по величине и направлению реакцию заменим двумя составляющими: RA – вертикальной, перпендикулярной оси балки, и ХА – горизонтальной, направленной по оси Х. На шарнирно-подвижной опоре В реакция RB направлена перпендикулярно оси балки.
Составляем следующую систему уравнений статики:
![]()
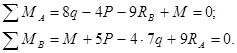
Решив ее при заданных исходных данных, получим
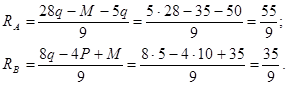
Для проверки составим еще одно уравнение статики, сумму проекций всех сил на ось Y
![]()
Следовательно, реакции определены верно.
Для построения эпюр Q и М необходимо определить поперечные силы и изгибающие моменты. Данная балка имеет два грузовых участка, границами которых являются опорные сечения и сечение, где приложена сосредоточенная сила Р. Чтобы составить уравнения Q и М, для каждого участка проводим произвольные сечения на расстоянии х от начала координат.
В качестве первого участка рассмотрим ту часть балки, на которую действует рассредоточенная сила q. На нем абсцисса х изменяется в пределах 0≤х1 ≤4.
Здесь Q1 =RA -qx1 ; Q1 =55/9кН при х1 =0; Q1 =-125/9кН при х1 =4м.
Уравнение моментов имеет вид
![]()
при х1 =0 М1 =0;
при х1 =4м М1 =-140/9кНм.
Для уточнения вида эпюры М на первом участке необходимо определить экстремальное значение М в сечении, где Q=0. Абсцисса этого сечения может быть вычислена из уравнения
Q1 =RA -qx=0.
Таким образом
![]() м.
м.
Подставив это значение в выражение М1 =RA x-qx2 /2, найдем Мmax =605/162=3,7кНм.
На втором участке абсцисса х меняется в пределах 4≤х2 ≤9. На этом участке Q2 =const и Q2 =RA +P-4q=55/9+10-20=-35/9. Уравнение моментов на этом участке имеет вид
![]() при х2 =4м М2 =55/9·4+4·5·2=-140/9кНм;
при х2 =4м М2 =55/9·4+4·5·2=-140/9кНм;