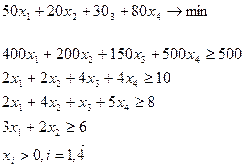Предположим, что будет изготовлено - булок, - пирожных, - ватрушек, - коржиков, - слоёнок. - прибыль булок, - пирожных, - ватрушек, - коржиков, - слоёнок, .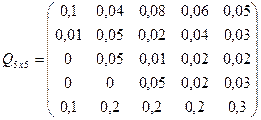

матрица затрат на производство. - удельные затраты на производство определённых изделий. - вид затрачиваемого ресурса, - вид конечного продукта.

Математическая модель в общем виде:

и

где - количество исходного ресурса на складе.

Математическая модель для нашей задачи:

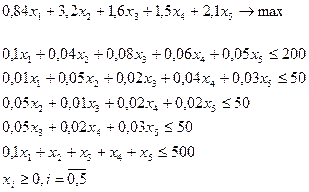
Задача 4

Содержательная постановка

На предприятии образовалось 150 м³ свободных остатков пиломатериалов и 1600 м² листового стекла. Эти материальные ресурсы можно использовать в цехе товаров народного потребления, к примеру, для производства сервантов, книжных полок и зеркал (маркетологи «дают добро» на возможность сбыта этих товаров по следующим ценам: сервант – 91, книжная полка – 14.5, зеркало – 11 денежных единиц), данные на затраты каждого ресурса приведены в таблице 1.

Ресурсы Продукция	Пиломатериалы, куб.м	Стекло, кв.м
Сервант	0.25	2.0
Книжная полка	0.05	0.5
Зеркало	0.025	0.4

таблица 1

Математическая модель

Предположим, что - кол-во сервантов, - книжных полок, - зеркал. - прибыль с продажи серванта , - книжной полки, - зеркало. матрица затрат на производство. - удельные затраты на производство определённых изделий. - вид затрачиваемого ресурса, - вид конечного продукта.

Математическая модель в общем виде:

и

где - количество исходного ресурса.

Математическая модель для нашей задачи:

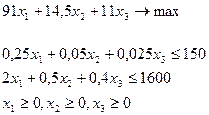
Задача 5

Содержательная постановка

Магазин оптовой торговли реализует три вида продукции: Молоко, мясо, хлеб. Для этого используются два ограниченных ресурса - полезная площадь помещений, которая с учётом оборачиваемости составляет 450 кв метров, и рабочее время работников магазина – 600 человеко-часов. Товарооборот должен быть не меньше 240 тыс. рублей. Необходимо разработать план товарооборота, доставляющий максимум прибыли. Затраты ресурсов на реализацию и получаемая при этом прибыль представлены в таблице 1.

Ресурсы	Затраты ресурсов на реализацию, тыс. руб			Объём ресурса
	Молоко	Мясо	Хлеб
Полезная площадь, км. м. Рабочее время, чел – ч.	1,5 3	2 2	3 1,5	450 600
Прибыль, тыс. р.	50	65	70

таблица 1

Математическая модель

Предположим, что - молоко, - мясо, - хлеб. - прибыль с молока, - мяса, - хлеба.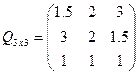 матрица затрат на производство. - удельные затраты на производство определённых изделий. - вид затрачиваемого ресурса, - вид конечного продукта.

Математическая модель в общем виде:

и

где - количество исходного ресурса.

Математическая модель для нашей задачи:

Задача 6

Содержательная постановка

Диета включает продукты 4 основных групп: сладости, домашняя еда, напитки, и фаст-фуд. В настоящее время доступны следующие представители этих групп : пирожные, 50с за шт., котлеты, 20с за шт., кола, 30с за бут., биг-мак, 80с за шт.

В единице продукта содержится следующее количество некоторых веществ, эти данные представлены в таблице 1:

	Калории	Сахар	Жир	витамины
Пирожное	400	2	2	3
Котлета	200	2	4	2
Кола	150	4	1	0
Биг-мак	500	4	5	0

таблица 1

Есть ограничения на вещества в день: Сумма калорий ≥ 500, сумма витаминов ≥ 6, сумма сахара ≥ 10, сумма жира ≥ 8. Надо получить набор, при котором человек будет получать необходимое число веществ, но стоимость этого набора должна быть минимальна.

Математическая модель

Предположим, что будет куплено - пирожных, - котлет, - бутылок колы, - биг-маков, - стоимость пирожных, - котлет, - бутылки колы, - биг-мака.

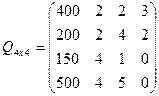
матрица показывающая содержание веществ. - количество определённого вещества. - вид продукта, - вид вещества.

Математическая модель в общем виде:

и

где - минимальное количество вещества в день.

Математическая модель для нашей задачи:

Задача 7

Содержательная постановка