Курсовая работа: Построение реалистичного изображения методом обратной трассировки лучей

где x₀ , y₀ , z₀ – координаты центра параболоида, A, B, C – длины полуосей параболоида. Ось параболоида расположена вдоль оси Oz мировой системы координат.

Для вычисления координат вектора нормали необходимо вычислить частные производные по x, y, z.

Координаты вектора нормали эллипсоида:

X_n = 2(x-x₀ )/A² ,

Y_n = 2(y-y₀ )/B² ,

Z_n = 2(z-z₀ )/С² .

Направление вектора не изменится, если все его координаты разделить на 2:

X_n = (x-x₀ )/A² ,

Y_n = (y-y₀ )/B² ,

Z_n = (z-z₀ )/С² .

Координаты вектора нормали параболоида вычисляются аналогично:

X_n = (x-x₀ )/A² ,

Y_n = (y-y₀ )/B² ,

Z_n = – (z-z₀ )/С² .

Нормаль для поверхности второго порядка придется вычислять непосредственно в теле трассировки, так как в разных точках фигуры нормали разные.

Вычисление отраженного луча

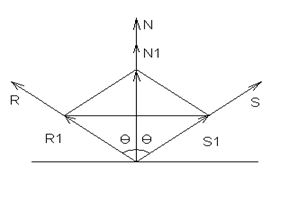
Пусть задан вектор падающего луча S, а также известен вектор нормали N. Требуется найти вектор отраженного луча R.

Рассмотрим единичные векторы R₁ , S₁ и N₁ . Поскольку векторы нормали, падающего луча и отраженного луча находятся в одной плоскости, то можно записать R₁ + S₁ = N`, где N` - это вектор, соответствующий диагонали ромба и совпадающий по направлению с нормалью. Длина вектора N` равна 2cosθ. Так как вектор N` по направлению совпадает с N₁ , то

N` = N`2cosθ.

Отсюда найдем единичный вектор отраженного луча:

R₁ = N₁ 2cosθ – S₁ = N/|N| 2cosθ – S/|S|.

Найдем cosθ. Это можно сделать, используя скалярное произведение векторов N и S:

cosθ = N*S/(|N|*|S|).

Полагая, что искомый вектор отраженного луча будет иметь такую же длину, что и вектор падающего луча, то есть R = |S| R₁ , получим

R = N 2NS/|N|² – S.

Это решение в векторной форме. Запишем координаты вектора:

x_R = 2x_N (x_N x_S +y_N y_S +z_N z_S )/(x_N ² +y_N ² +z_N ² ) – x_S ,

y_R = 2y_N (x_N x_S +y_N y_S +z_N z_S )/(x_N ² +y_N ² +z_N ² ) – y_S ,

z_R = 2z_N (x_N x_S +y_N y_S +z_N z_S )/(x_N ² +y_N ² +z_N ² ) – z_S .

Вычисление преломленного луча