Курсовая работа: Применение производной и интеграла для решения уравнений и неравенств

Сумма равна сумме площадей прямоугольников, построенных на отрезках как на основаниях, с высотами , т.е. равна площади ступенчатой фигуры «вписанной» в криволинейную трапецию. Так как функция f возрастает, то эта площадь меньше площади криволинейной трапеции. Отсюда

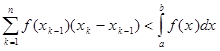(2.1)

Аналогично, рассматривая площадь «описанной» ступенчатой фигуры, получаем

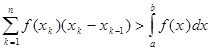(2.2)

Если функция f положительна, непрерывна и убывающая на [a,b], то

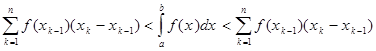(2.3)

Покажем на ряде примеров, как соотношения (2.1)-(2.3) используются при доказательстве неравенств.

Задача 2.1. Доказать, что если , то .

Решение.

Выражение совпадает с левой частью неравенства (2.1), где . Функция на интервале возрастает, непрерына, положительна. Поэтому, согласно (1), 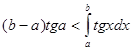. Функция является первообразной для функции , так как

. Поэтому 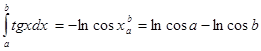. Левая часть двойного неравенства доказана. Правая часть получается из соотношения (2.2) для функции при тех же предположениях.

При решении задачи 1 мы использовали тот факт, что площадь криволиней-ной трапеции, ограниченной графиком непрерывной, положительной, возрастаю-щей на [a,b] функции , отрезком [a,b] оси x и прямыми , заключена между площадями прямоугольников, построенных на [a,b] как на основании, с высотами и соответственно.

Площади прямоугольников дают, вообще говоря, довольно грубые приближения для площади криволинейной трапеции. Более точные оценки получаются путем разбиения отрезка [a,b] на достаточно большое число частей.

Задача 2.2. Пусть . Доказать, что для каждого .

Решение.

Рассмотрим и функцию . Она непрерывна, положительна и убывающая. Воспользуемся неравенством (2.3), где . (Точки делят отрезок на отрезки одинаковой длины ). Получим

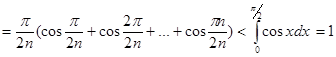
Отсюда . Кроме того,

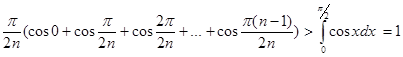, т.е.

.

В приведенном решение выражение для легко представлялось в виде площади некоторой ступенчатой фигуры. Чтобы воспользоваться рассмотренным в задаче методом доказательства неравенств, чаще приходится предварительно преобразо-вывать выражения, встречающиеся в неравенствах.

Задача 2.3. Доказать, что для каждого натурального n .

Решение.

Левую часть неравенства при можно представить в следующем виде:

Рассмотрим функцию на отрезке .Этот отрезок точками , разбивается на n равных частей длины 1. Выражение

равно сумме площадей прямоугольников, построенных на отрезках как на основаниях с высотами . Функция при

положительна, непрерывна, убывающая. Поэтому можно воспользоваться неравенством (2.3). Имеем