Курсовая работа: Применение производной и интеграла для решения уравнений и неравенств

Из определения интеграла вытекает, что для неотрицательной непрерывной на отрезке [a,b] функции f 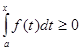для всех .

Теорема 1. Пусть функции f и g непрерывны на отрезке [a,b] и для всех . Тогда для всех : . Это свойство называют монотонностью интеграла.

С помощью теоремы 1 почленно проинтегрировав обе части неравенства, можно получить целую серию новых неравенств. Например,

при имеем очевидное неравенство . Применим теорему 1, положив . Функции f, g удовлетворяют условиям теоремы на промежутке . Поэтому для произвольного : , т.е. (1). Применяя тот же метод к неравенству (1), получаем , или . Отсюда . Продолжая аналогично, имеем ,

и т.д.

В рассмотренном примере выбор исходного неравенства не составил труда. В иных случаях этот первый шаг решения задачи не столь очевиден. Теорема 1 дает, по существу, прием для получения исходного неравенства.

Пусть требуется проверить истинность неравенства

(2.4)

Если справедливо соотношение , то согласно теореме 1, имеет место и неравенство

, или (2.5).

Если имеет место неравенство , то, складывая его почленно с (2.4), устанавливаем справедливость неравенства (2.5).

Задача 2.4. Доказать, что при . (2.6)

Решение.

Неравенство (2.6) перепишем в виде . Левая и правая части последнего неравенства представляют собой функции от . Обозначив , получим (2.7). Докажем, что (2.7) выполняется при . Найдем производные обеих частей неравенства (2.7). Соответственно имеем:

. При . Действительно, . Применяя теорему 1 для функций и при , получаем . Так как , то

. Отсюда при , следует (2.6).

Задача 2.5. Доказать, что при : .

Решение.

Вычислим производные левой и правой частей:

Ясно, что , поскольку , . Так как и непрерывные функции, то, согласно теореме 1, имеет место неравенство

, т.е. , . Задача 2.5. решена.

Теорема 1 позволяет устанавливать истинность нестрогих неравенств. Утверждение, содержащееся в ней, можно усилить, если потребовать выполнения дополнительных условий.

Теорема 2. Пусть выполняются условия теоремы 1 и, кроме того, для некоторого имеет место строгое неравенство . Тогда при также имеет место строгое неравенство .

Задача 2.6. Доказать, что при : (2.8).

Решение.

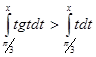Предварительно следует проверить соответствующее неравенство для производных левой и правой частей, т.е. что , или . Его справедливость при можно установить, если применить теорему 1 к неравенству . Поскольку, кроме того, , то выполняются все условия теоремы 2. Поэтому имеет место строгое неравенство , , или 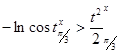, . После преобразований придем к неравенству (2.8).

2.3. Интегралы от выпуклых функций

При решении многих задач целесообразно применять следующий подход.

Разделим отрезок [a,b], на котором задана непрерывная функция f. на n частей точками . Построим прямоугольные трапеции, основаниями которых являются отрезки xkyk, xk+1yk+1, а высотами – xkxk+1, k=0,1,…,n-1. Сумма площадей этих трапеций при достаточно большом n близка к площади криволинейной трапеции. Чтобы этот факт можно было применить к доказательству неравенств функция f должна удовлетворять некоторым дополнительным требованиям.

Пусть функция f дважды дифференцируема на некотором промежутке и в каждой точке этого промежутка f//(x)>0. Это означает, что функция f/ возрастает, т.е. при движении вдоль кривой слева направо угол наклона касательной к графику возрастает. Иными словами, касательная поворачивается в направлении, обратном направлению вращения часовой стрелки. График при этом «изгибается вверх», «выпячиваясь вниз». Такая функция называется выпуклой. График выпуклой функции расположен «ниже» своих хорд и «выше» своих касательных. Аналогично, если f//(x)<0, то f/ убывает, касательная вращается по часовой стрелке и график лежит «выше» своих хорд, но «ниже» своих касательных. Такая функция называется вогнутой.