Курсовая работа: Привод с цилиндрическим одноступенчатым вертикальным косозубым редуктором

,

где s_{F lim j} - предел выносливости зубьев при изгибе (табл. 7),

s_{F lim 1} =1.75•HB₁ =1.75•262 = 458.5 МПа, s_{F lim 2} = 1.75•207 = 362.25 МПа.

S_Fj - коэффициент безопасности при изгибе (табл. 7): S_{F 1} = 1.7, S_{F 2} =1.7

K_FLj - коэффициент долговечности при изгибе:

К_FLj =,

q_j – показатели степени кривой усталости: q₁ = 6, q₂ = 6 (табл. 6);

N_FO – базовое число циклов при изгибе; N_FO = 10⁶ .

N_FEj – эквивалентное число циклов напряжений при изгибе; N_{FE j} = N_{У j Fj.}

Коэффициент эквивалентности при действии напряжений изгиба – _Fj определяется по табл. 6 в зависимости от режима нагружения и способа термообработки: _F1 =0.038, _F2 = 0.038,

N_{FE 1} = 1424586240•0.038 = 54134277,12; N_{FE 2} = 401179968•0.038 = 15244838,78

Поскольку N_FE > N_FO , принимаем

К_FL1 = 1, К_FL2 = 1;

K_FCj - коэффициент, учитывающий влияние двухстороннего приложения нагрузки для реверсивного привода, K_{FC 1} = 0.65, K_{FC 2} = 0.65.

Допускаемые напряжения изгиба: s_{F P 1} = 175.309 МПа, s_{F P 2} = 138.507 МПа.

Межосевое расстояние определяем из условия контактной прочности:

a_w = K_a •(u + 1) ,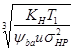

редуктор передача электродвигатель агрегат

где K_a – коэффициент вида передачи, K_a = 410 для косозубых передач,

ш_ba – коэффициент ширины венца по межосевому расстоянию, выбираем из ряда по ГОСТ 2185–66 с учетом расположения опор относительно зубчатого венца ш_ba = 0.4,

К_Н - коэффициент контактной нагрузки, принимаем на этапе проектного расчета К_Н =1.2.

Расчетное межосевое расстояние a_w = 123.69 мм. Полученную величину округлим до ближайшего стандартного значения (табл. 2): a_w =125 мм.

Находим ширину колеса и шестерни по формулам: b_{w 2} = ш_ba a_w =0.4•125=50_,

b_{w 1} = b_{w 2} +2…5=50+4 =54. Полученные значения округляем до ближайшего числа из ряда нормальных линейных размеров по ГОСТ 6636–69: b_{w 1} = 54 мм, b_{w 2} = 50 мм.

Модуль выбираем из диапазона m=(0.01…0.02)•a_w =(1,25…2,5) и округляем до стандартного значения по ГОСТ 9563–60 (табл. 1), учитывая, что применение модуля меньше 2 мм для силовых передач не рекомендуется: m= 2,5.

Для косозубых передач стандартизован нормальный модуль m_n =m = 2,5.

Суммарное число зубьев: для прямозубой передачи Z=, для косозубой передачи Z=, где b₁ – начальный делительный угол наклона зуба(=12 для косозубых передач).

Суммарное число зубьев получим округлением Z=97,81 до ближайшего целого числа: Z_У = 98.

Для косозубых и шевронных передач определяем делительный угол наклона зуба по формуле = 11⁰ 28’42’’. Число зубьев шестерни и колеса, а также уточненное передаточное отношение равны: