Курсовая работа: Проект системы автоматического управления температуры печи
Качества процесса регулирования. На этот вопрос нам поможет ответить переходная характеристика системы, приведенная ниже.
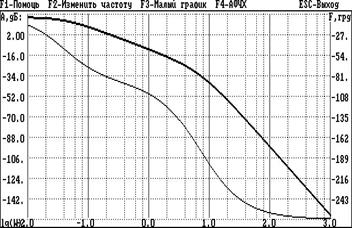
Рисунок 4 - ЛАЧХ и ЛФЧХ исходной САУ
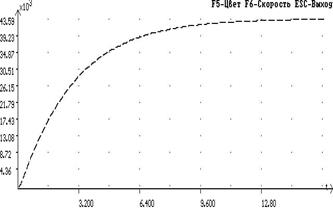
Рисунок 5 - переходная характеристика, исходной, САУ.
Исходная система в разомкнутом состоянии устойчива ,так как ЛАЧХ пересекает ось абсцисс раньше, чем ЛФЧХ пересекает линию, соответствующую фазовому сдвигу -π. Система находится в устойчивом состоянии, но не удовлетворяет заданным перерегулированию и времени переходного процесса.
4. Синтез корректирующих устройств САУ
Исходя из данных показателей качества переходного процесса, построим "желаемую" ЛАЧХ. Качество процессов регулирования в основном определяется ОСЧ, где находится частота среза юср. озер выбирается в зависимости от нужного быстродействия системы (tp) и перерегулирования (σ)
ωср = βπ/ tp
β зависит от σ и выбирается из справочника по номограммам.
Для данной системы σ = 20 %, tp= 1 с; β из справочника берем равным 1,7. Следовательно,
ωср = 1,7*3,14/1= 5,341 (с-1)
ωк2= 2…4ωср =10,682…21,363 (с-1) принимаем 10
ωк1=ω2ср/ ωк2 = 1,902 (с-1) принимаем 0,8
В результате исследований установлено, что наклон желаемой ЛАЧХ вблизи ωср должен быть равным - 20дБ/дек.
В области низких частот у «желаемой» ЛАЧХ оставляем наклон -20дБ/дек. В области высоких частот «желаемая» ЛАЧХ повторяет исходную ЛАЧХ, т.к. ОВЧ не оказывает существенного влияния на характеристики системы. Построение «желаемой» ЛАЧХ приведено на рисунке выполненном на миллиметровой бумаге.
По этим данным определяем, что корректирующим звеном является два интегро-дифференцирующих звена. Передаточная функция получившегося звена имеет вид:
Wk(p) =
Переходная характеристика при таком корректирующем звене имеет следующий вид:
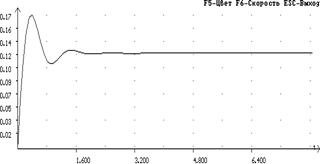
Рисунок 8 - переходный процесс скорректированной
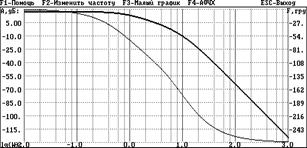
Рисунок 9 - ЛАЧХ и ЛФЧХ скорректированной САУ.
Найдем вид данного звена.
В качестве звена будем использовать пассивные четырехполюсники постоянного тока:
Рассчитаем параметры элементов.
Для первого четырехполюсника:
T1=25 ; T2 = 1,25;
W(p) =k1(T1p+1) / (T2p+1) ; k1 = C1 / (C1 + C2); T2 = k1*T!; T1= R*C2 =>