Курсовая работа: Проектирование электронной пушки

При помощи рассмотренной пушки Пирса можно получать сходящиеся электронные пучки с первеансом Р£ 1 мкА/В. При малых значениях первеанса коэффициент сходимости по плотности может составлять 100 и более, как, например, в пушке, разработанной в лаборатории радиотехнической электроники ЛЭТИ им. В. И. Ульянова (Ленина) (см.рис.1.1). При больших значениях Р коэффициент сходимости обычно составляет несколько единиц.

Для получения сходящихся потоков с - более высоким первеансом используют различные модификации пушек Пирса (рис. 1.2). Они характеризуются относительно небольшими расстояниями катод—анод и применением прикатодных электродов закрытой конструкции (см. рис. 1.2). Благодаря таким электродам электрические поля пушек более эффективно компенсируют поперечные расфокусирующие силы пространственного заряда, возрастающие по мере повышения первеанса, и тем самым обеспечивают формирование высокопервеансных сходящихся пучков с минимальными потерями катодного тока на аноде (не более 1—2%). Однако из-за влияния анодных отверстий пушек, заметно ослабляющих поля в центре катодов и работающих как рассеивающие линзы со сферической аберрацией, формируемые ими пучки оказываются неламинарными, с неравномерным распределением плотности тока по радиусу пучков.

2. Проектирование и особенности конструкции пушек, формирующие цилиндрические и ленточные пучки

Физические принципы, на которых базируются пушки Пирса, используются для формирования не только сплошных сходящихся (конических) электронных пучков, но также цилиндрических, плоских (ленточных и клиновидных), трубчатых (полых) пучков.

Формирование параллельного ленточного пучка. Электронная пушка, формирующая параллельный ленточный пучок, может быть создана путем использования части плоскопараллельного потока, который характеризуется соотношениями:

2.1 2.2

где z—продольная координата, отсчитываемая от катода(рис. 2.1); А=U_a /d^4/3 при z=d, U=U_a .

2.3

???? ?? ?????? ?????? ???????? ???? ???????? 2?_n , ?? ??? ?????????? ????????? ???????? ?????????? ? ???? ???? ??????????, ????? ?? ??? ???????? ??????????? ??????? ??? ?==0:

2.1

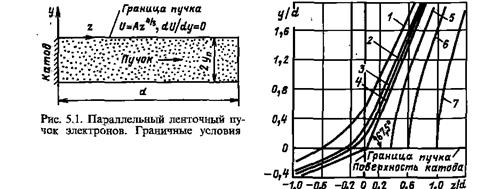
Рис. 2.2. Форма эквипотенциальных линий, получающихся в результате расчета внешней задачи для параллельного ленточного пучка электронов и потенциалов: 1— -0,25 U_a 2— -0,1 U_a 3— -0,05U_a 4—0; 5—0,25U_a 6—0,5U_a 7—U_a

Решение задачи Коши для уравнения Лапласа в области,, внешней к катоду, которое удовлетворяет условиям (2.3), находится методом аналитического продолжения функции и имеет вид

2.4

Форма эквипотенциальных линий, определенная с помощью этого выражения, представлена на рис. 2.2. Нулевая эквипотенциаль является прямой линией, наклоненной к границе пучка под углом 67,5°. Полученные результаты строго справедливы для потока, имеющего бесконечную протяженность в направлении, перпендикулярном плоскости чертежа (в направлении оси х). С определенным приближением они могут быть использованы для потоков конечной ширины, при условии, что ширина потока х_п >>2y_п и влияние краевых эффектов незначительно. Первеанс такой пушки, рассчитанный на единицу ширины потока, находится из закона “степени 3/2”:

Анодный электрод реальной пушки обычно имеет отверстие, не закрытое сеткой (рис.2.3). Отверстие нарушает распределение электрического поля, положенное в основу описанного выше расчета, приводит к появлению y-составляющей поля вблизи анодного электрода и уменьшению z-составляющей поля в области катода. Это в свою очередь приводит к появлению у электронов на выходе из пушки y-составляющих скоростей и уменьшению первеанса потока (при 2у_п @d). Расфокусирующее действие анодного отверстия можно учесть, если рассматривать его как щелевую линзу. Фокусное расстояние последней определяется выражением f=2U/(Е1—Е2), где U—потенциал электрода щелевой линзы (он принимается равным потенциалу анода U= U_a ); Е1 и Е2 напряженности поля слева и справа от электрода при отсутствии в нем отверстия. В рассматриваемом случае Е2=0, а Е1 рассчитывается следующим образом:

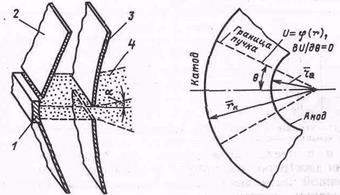
Рис. 2.4. Клиновидный ленточный пучок. Граничные условия

В этом случае получаем f= — 3/2d. Отрицательная величина фокусного расстояния указывает на рассеивающий характер линзы. Для угла наклона граничной электронной траектории на выходе из пушки получаем следующую приближенную формулу:

и для граничных электронов:

Формирование клиновидного пучка. Электронная пушка для формирования клиновидного (сходящегося) пучка может быть построена путем использования части радиального цилиндрического потока (рис. 2.4). Такой поток характеризуется следующими основными соотношениями: распределение потенциала

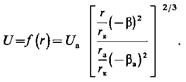
Ток в секторе, имеющем единичную ширину (размер в направлении оси r) и половинный угол q (угол в градусах),

где (—b)² —функция отношения радиуса кривизны катода r_к к текущему радиусу r.

Как и в предыдущем случае, для сохранения характера движения электронов в секторе с половинным углом q действие отброшенной части электронного потока заменяется действием фокусирующих электродов, которые должны обеспечивать выполнение вдоль границы пучка следующих условий: U=f(r), дU/дq=0. Форма фокусирующих электродов находится в результате решения внешней задачи синтеза. На рис. 2.5 показано семейство эквипотенциальных линий, найденное аналитически.

Влияние анодного отверстия в анодном электроде на отбор тока с катода и формирование пучка аналогично рассмотренному в предыдущем случае.

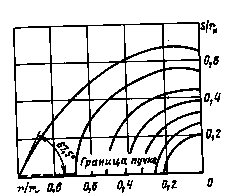
Рис.2.5. Универсальная карта эквипотенциалей для расчета электродов пушки, формирующей клиновидный ленточный пучок.

Формирование параллельного цилиндрического пучка. Задача формирования параллельного цилиндрического пучка решается аналогично рассмотренной выше задаче формирования параллельного ленточного пучка, с той лишь разницей, что из бесконечного параллельного потока «вырезается» область в виде цилиндра (рис. 2.6). Для определения формы фокусирующих электродов решается внешняя задача при следующих начальных условиях, заданных на границе области:

, .