Курсовая работа: Проектирование модели для определения времени простоя станков на машиностроительном предприятии

2. Каждому календарному расписанию приписываем его оценку в виде минимально возможного времени окончания Обработки деталей на последнем станке n в предположении, что на первых п — 1 станках конфликты отсутствуют.

Из матрицы известно возможное время начала обработки любой детали i на последнем станке. Оно совпадает с временем окончания ее обработки на предпоследнем станке.

Чтобы не увеличивать длительность обработки деталей, целесообразно на последнем станке обрабатывать детали в очередности их поступления на этот станок

,

где

Оценка определяется следующим образом.

Первоначально сравниваем с .

Если , то время завершения обработки двух деталей i₁ и на последней операции будет равно времени окончания обработки детали i₂ , т. е.

.

Если , то .

Далее сравниваем время завершения обработки на последнем станке двух первых деталей i₁ и i₂ с временам завершения обработки на предпоследнем стачке детали i₃ .Здесь возможны два случая:

1) если., то ;

2) если , то , и т.д.

В результате такого цепного расчета получим минимально возможное время обработки всех деталей для варианта расписания предположении, что все конфликты в нем на первых п — 1 станках устранены. Эту величину и принимаем за нижнюю границу времени окончания обработки деталей по расписанию

.

Как видно из матрицы , моменты завершения обработки деталей на предпоследнем, втором станке упорядочены следующим образом:

,

т. е. детали на последний станок поступают в очередности 1, 3, 2, 4. Выбираем первые две детали 1 и 3 и определяем момент завершения их обработки на последнем станке.

Так как , то .

Включаем в рассмотрение третью по порядку деталь 2. Поскольку, то минимально возможное время обработки первых трех деталей (1, 3, 2) будет

.

Рассматривая последнюю деталь, видим, что .

Следовательно, .

Отсюда получаем

.

Повторим действия I и 2 для остальных вариантов, когда первой на первом станке обрабатывается деталь 2, 3 или 4.

Разрешая конфликт в пользу детали 2, получаем

, .

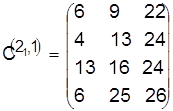Отдавая предпочтение па первом станке детали 3, получаем расписание и его опенку в виде

, .

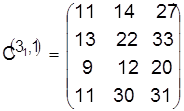Разрешаем конфликт в пользу детали 4:

, .

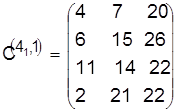3. Сопоставляем расписания , и их оценки с вершинами дерева, изображающего процесс ветвления всего множества вариантов расписания на подмножества (рисунок 1).

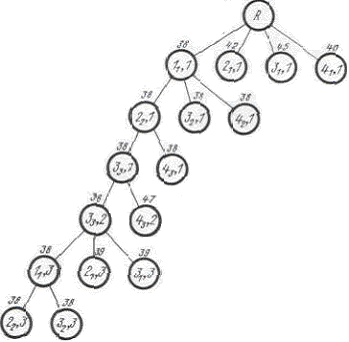
Рисунок 1

Из всех рассмотренных календарных расписаний выбираем такое , для которого

.

Поскольку наименьшей оценкой является , предпочтение к запуску на первом станке отдается детали l=1. Остальные m-1=3 детали продолжают конфликтовать па первом станке.

Четвертый шаг. В качестве исходного календарного расписания для дальнейших расчетов берем матрицу , на основе которой будем определять деталь, подлежащую запуску на нервом станке второй. Для этого построим календарные расписания в виде матриц , элементы которых находятся по правилу

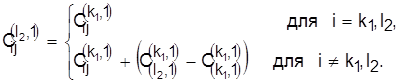
Разрешая конфликты для каждой из т—1 оставшейся детали на первом станке, получим нижнюю границу для каждого расписания и выберем из всех расписаний то, для которого

.

Детальk₂ планируется к обработке второй. Выполним эти расчеты для нашего примера.

Разрешая конфликт для детали 2, построим для нее календарное расписание с учетом того, что деталь 1 уже назначена к обработке первой, и найдем его нижнюю границу. Получим

, .

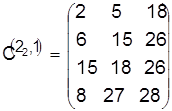Разрешаем конфликт в пользу детали 3:

, .
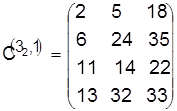