Курсовая работа: Проектирование модели для определения времени простоя станков на машиностроительном предприятии
Сопоставим полученные расписания и их оценки с вершинами дерева, разливаемыми из вершины 
(рисунок 1).
Так как оценки для всех вариантов одинаковы, безразлично, какой из деталей отдать предпочтение. Пусть деталь 2 планируется к запуску на первом станке второй.
Пятый шаг. Аналогичным образом определим деталь, запускаемую на первом станке третьей.
Разрешаем конфликт относительно детали 3:
, 
.
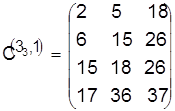Разрешаем конфликт относительно детали 4:
, 
.
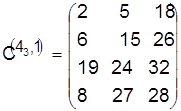Сопоставляем полученные расписания и их оценки с вершинами дерева, развиваемыми из вершины 
(рисунок 1). Так как оценки, связанные с запуском на первом станке трех первых детален в очередности 1, 2, 3 или 1, 2, 4, одинаковы, безразлично, какой из них отдать предпочтение. Пусть выбрана первая из них, k3 =3, тогда последовательность обработки деталей на первом станке будет 1, 2, 3, 4, с нижней границей, равной 38.
Шестой шаг. В результате предыдущих шагов получено календарное расписание 
и последовательность запуска партий деталей на первом станке 
.
Далее провернем и последовательно разрешаем конфликты на втором станке.
Детали 1, 2, 3, 4 планируются к обработке в интервалах времени соответственно (2—5), (6—15), (15—18),(17—36).
Следовательно, на втором станке деталь 2 запускается после детали I, а детали 3 и 4 конфликтуют.
Разрешим конфликт относительно детали 3.
Для этого на базе 
составим расписание, в котором элементы 
для данной детали и деталей, не участвующих в конфликте, остаются без изменения, а элементы 
и 
возрастают на величину задержки в поступлении детали 4 на второй станок, которая равна в данном случае разности 
—
== 1. Получим расписание и оценку нижней границы:
, 
.
Разрешая конфликт в пользу детали 4, задерживаем подачу детали 3 ко второму станку на 36—15=21, в результате чего расписание и его оценка принимают вид
, 
.
Сопоставляя эти расписания и оценки с вершинами графа, развиваемыми из вершины 
, выбираем расписание 
, предусматривающее обработку на втором станке третьей по порядку детали 3.
Таким образом, на этом шаге упорядочена очередность запусков партий на втором станке в виде последовательности деталей 1. 2, 3, 4 с оценкой времени совокупного цикла 
.
Седьмой шаг. Отправляясь от расписания , проверяем наличие конфликтующих детален на третьем станке.
Детали 1, 2, 3, 4 планируются к обработке в интервалах времени соответственно (5—18), (15—26), (18—26),(37—38).
Конфликтуют три первые детали. Разрешаем конфликт в пользу детали 1:
, 
.
Разрешаем конфликт в пользу детали 2:
, 
.
Разрешаем конфликт в пользу детали 3:
, 
.
Разветвляем вершину дерева решений (рисунок 1) в соответствии с полученными оценками. Для определения детали, запускаемой па третьем станке второй, выбираем расписание 
, имеющее меньшую нижнюю границу.
Рассматривая его, видим, что на третьем станке конфликтуют детали 2 и 3, обрабатываемые в интервалы времени соответственно (15—29) и (18—26).
Разрешим конфликт, отдавая предпочтение детали 2.
Получим расписание и его оценку:
, 
.
Разрешим конфликт в пользу детали 3:
, 
.
Таким образом, безразлично, какой детали отдать предпочтение. Пусть второй обрабатывается деталь 2. Проверяя расписание 
, устанавливаем отсутствие конфликтов па третьем станке.
Мы нашли один из вариантов календарного расписания. Чтобы убедиться в его оптимальности, рассмотрим дерево ветвлений и проанализируем значения нижних границ для всех его оборванных ветвей. Поскольку все нижние оценки не меньше полученной, считаем расписание оптимальным. Начало времени обработки партий деталей
.
Календарный график работы оборудования, соответствующий расписаниям 
и А..
Цифры над прямоугольниками — номера деталей, внутри прямоугольника — время начала и окончания обработки партии деталей.