Курсовая работа: Проектирование узла цифрового комбинационного устройства

Рисунок 1 – Схема полученной СДНФ

1.4 Составление схемы СКНФ

Составляем схему полученной СКНФ с помощью базисных элементов И, ИЛИ, НЕ:

Рисунок 2 – Схема полученной СКНФ

2 . Минимизация логической функции методом Квайна

Метод основан на операциях склеивания и поглощения. Операция склеивания производится по правилу: Z(X+X) = Z, где Z произвольная комбинация символов. Операция поглощения выполняется по правилу: М(1+Х)=М. Сначала выполняется операция склеивания, затем операция поглощения. При поглощении из логического выражения удаляются все члены, поглощенные членами, полученными при склеивании.

Находим МДНФ (минимальную дизъюнктивную нормальную форму). Для этого с помощью операции склеивания из СДНФ сначала получаем сокращенную форму:

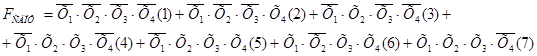
Здесь и далее индексы в скобках — это порядковые номера минтерм, которые используются для большей наглядности проводимых преобразований.

Выполним операцию попарного склеивания:

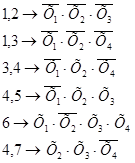
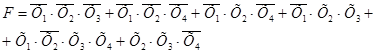
Получили сокращенную форму, строим импликантную матрицу:

Таблица 2

Простые импликанты	Члены СДНФ
	Х	Х
	Х	Х
	Х	Х
	Х	Х
	Х
	Х	Х

В левом столбце таблицы 2 записываем члены сокращенной формы (простые импликанты), в верхней строке – члены СДНФ. В минимальную форму войдут те члены сокращенной формы, с помощью которых можно представить все члены СДНФ. Из матрицы видно, что не все члены сокращенной формы войдут в минимальную ДНФ:

Находим МКНФ (минимальную конъюнктивную нормальную форму).

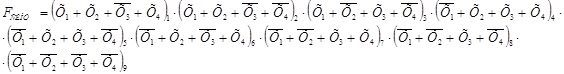
Здесь и далее индексы - это порядковые номера макстермов, которые введены для большей наглядности проводимых преобразований.

Далее выполним операцию попарного склеивания:

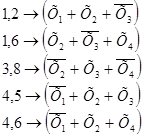
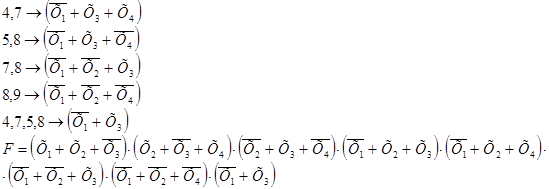
Таблица 3 - Импликантная матрица

1	2	3	4	5	6	7	8	9
	Х	Х
	Х	Х
	Х	Х
	Х	Х
	Х	Х
	Х	Х
	Х	Х
	Х	Х	Х	Х

3 Составление схем полученных МДНФ и МКНФ с помощью базисных элементом И, ИЛИ, НЕ

Рисунок 3 – Схема МКНФ