Курсовая работа: Программа вычисления минимума заданной функции
Выбор метода: Для решения задачи одномерной оптимизации существует множество методов, среди которых:
1) метод прямого перебора
2) метод дихотомии
3) метод золотого сечения
4) метод Фибоначчи
5) метод касательных
6) метод Ньютона
оптимизация методом квадратичной интерполяции Выберем метод дихотомии, т.к. он прост в алгоритмизации, обеспечивает быструю сходимость (на каждой итерации отрезок неопределённости сужается почти вдвое). Его недостаток в виде необходимости многократного вычисления F(x) не играет особой роли, т.к. F(x) – обыкновенный полином и расчёт его значений не затратит много ресурсов ПК.
Описание метода:
Пусть f(x)- унимодальная на [a;b] и требуется найти минимум f(x) с абсолютной погрешностью Е. Идея метода дихотомии состоит в проведении на каждой итерации двух отсчётов (вычислений значений функции), отстоящих от середины отрезке неопределённости [а;b] на величину de[0;2E] и сравнения значения исследуемой функции в двух точках х( n -1) и
x( n -1) . определяемых рекуррентными формулами:
Если
![]() , то
, то ![]()
![]()
Иначе
![]()
![]()
N = 1,2,...- номер итерации, а0 =а , b0 = b .
Вычисления проводятся до тех пор, пока b-а >Е.
Тогда с абсолютной погрешностью, не превосходящей Е, полагают
x* =(aN +bN )/2
Длина конечного отрезка неопределённости:
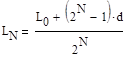
L0 =b-a – длина начального отрезка
На каждой итерации отрезок неопределённости [aN ;bN ] уменьшается примерно вдвое. Число отсчётов функции n и число итераций N связаны соотношением N=n/2
Практически величина d выбирается из условий различимости двух отсчётов функции
Процедура поиска минимума методом дихотомии использует большее количество отсчётов функции для локализации точки минимума на отрезке заданной длины.
Геометрическая иллюстрация метода дихотомии
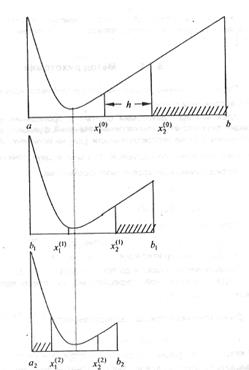
4. Проверка условий сходимости методов. Поиск значений интерполяционного многочлена в точках x 1 и x 2
Для правильной работы этого метода необходимо, чтобы функция была ограничена на отрезке интерполирования. Выполнение этого условия очевидно по заданию.