Курсовая работа: Проявление сил инерции на Земле

Таким образом, вес тела в системе отсчета, движущейся относительно земли с ускорением, отличается от произведения mg_φ , т.е. от веса тела на поверхности земли. Если сила Кориолиса невелика (при малой скорости движения тела относительно земли), то ее можно не учитывать. Тогда

(1.11)

где g* - напряженность результирующего поля сил тяготения и инерции в системе отсчета К'.

Формула (1.10) определяет вес тела в самом общем случае, а формула (1.11) - при условии, что силой Кориолиса можно пренебречь. Для величины g_φ берут среднее значение ускорения свободного падения g_φ = g = 9,81 м/с² . Формула (1.11) справедлива для опоры или подвеса любого вида.

Перегрузки и невесомость . Если модуль веса тела |Р| в (1.11) превосходит вес тела, покоящегося на земле (mg), то говорят, что внутри движущейся системы отсчета (например, самолета или космического корабля) установилось состояние перегрузки. Количественно перегрузка nвыражается так:

Десятикратная (n= 10) кратковременная перегрузка является пределом для человека (тренированного космонавта). Допустимое значение длительных перегрузок меньше. Имеющиеся для человека ограничения в перегрузках создают серьезные затруднения в использовании космических пилотируемых кораблей для исследования других (даже самых близких) звездных систем.

Чтобы космонавт мог в течение своей жизни (60 лет) достигнуть самой близкой к нам звезды α-Центавра, удаленной от Земли на расстояние, равное четырем световым годам, космический корабль должен как можно быстрее набрать скорость, соизмеримую со скоростью света. Расчет показывает, что необходимое для этого ускорение создает такую перегрузку, которую человек не сможет вынести, если не будут разработаны специальные защитные меры.

Если система отсчета (космический корабль, например) движется с ускорением а = g, то вес тела согласно (1.11) равен нулю (Р = 0), т.е. тело в этом случае не действует на опору; значит, напряженность результирующего поля сил гравитации и сил инерции в движущейся системе равна нулю (g*=0). Такое состояние и называют состоянием невесомости. Внешним проявлением этого состояния является отсутствие веса у тел. Однако дело не только в этом. При невесомости все тела находятся в особом, недеформированном состоянии. Это обусловлено тем, что в условиях невесомости нет ни массовых сил (g* = 0), ни сил реакции со стороны опоры, т.е. тех сил, которые создают деформацию покоящихся тел.

Для наблюдателя, находящегося в неподвижной (инерциальной) системе отсчета, все тела внутри ракеты и сама ракета или космический корабль свободно "падают" с одинаковым ускорением g. Именно поэтому они находятся друг относительно друга в покое и не оказывают давления друг на друга. По этой же причине частицы одного и того же тела не смещаются относительно друг друга и тело не деформируется. Таким образом, чтобы в ракете была невесомость, она должна двигаться свободно с ускорением g.

Этим способом создают "бассейн" невесомости при тренировках космонавтов. Просторный самолет сначала разгоняют до максимально допустимой скорости v₀ , образующей с горизонтом некоторый угол α, а затем выключают двигатели. При этом самолет совершает свободный полет по кривой, близкой к параболе. Отличие от параболы обусловлено наличием сопротивления воздуха. Чтобы движение происходило точно по параболе, двигатели выключают не полностью: они должны создавать тягу, которая компенсирует сопротивление воздуха. Так удается получить невесомость в течение малого промежутка времени.

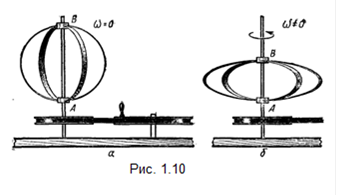
Деформация Земли . На вращающейся Земле центробежная сила действует не только на тело, лежащее на Земле, но и на каждую частицу самой Земли. Действие этих сил привело к тому, что Земля оказалась деформированной, сжатой у полюсов. Сжатие шарообразного тела у полюсов можно проиллюстрировать на следующей модели. Два круговых обруча из тонких полосок стали насажены на вертикальный стержень (рис.1.10, а). В нижней части обручи скреплены со стержнем. В верхней (В) они свободно могут скользить по стержню. Если привести обручи во вращение, то под действием центробежных сил они сожмутся в направлении оси вращения (рис.1.10,6).

В результате сплюснутости Земли ее полярная ось почти на ¹ /₃₀₀ долю короче диаметра экватора. А это приводит к тому, что и сила тяготения вблизи поверхности Земли становится зависящей от широты: она наибольшая на полюсе и наименьшая на экваторе. Поэтому фактическая зависимость g_φ от φ будет более сложной, чем это выражено соотношением (1.8), в котором ускорение g_o . сообщаемое телу силой тяготения, принималось не зависящим от широты. Измерения на различных широтах привели к следующей эмпирической формуле:

(1.12)

Здесь g_φ выражается в метрах на секунду в квадрате (м/с² ). Поправочный член достигает наибольшей величины при φ= 0, т.е. на экваторе, и достигает значения 0,052 м/с² . Ввиду малости этой величины ее влиянием в ряде случаев можно пренебрегать. При расчетах часто берут значение g_φ на уровне моря для широты φ = 45° (g_45° = 9,81 м/с² ).

Проявление сил Кориолиса . На любое тело, движущееся по поверхности Земли, действует кориолисова сила

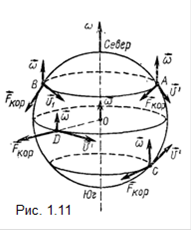
На рисунке 1.11 показаны силы Кориолиса для различных движений. В точке А тело движется с севера на юг. На него действует сила Кориолиса F_{ко p} , направленная на запад - вправо относительно направления v'. Если бы тело двигалось с юга на север, то F_{к op} была бы направлена на восток - снова вправо относительно v'. В точке В , находящейся также в северном полушарии, тело движется на восток, а кориолисова сила направлена на юг - опять вправо относительно v'. В точке С, находящейся в южном полушарии, сила Кориолиса направлена влево относительно скорости v'.

Если тело движется на экваторе и с юга на север или с севера на юг, то F_кор = 0, так как ω|| v'. Если же тело на экваторе движется с запада на восток (точка D), то сила Кориолиса направлена вертикально вверх; при движении с востока на запад эта - сила направлена вертикально вниз. Таким образом, силы Кориолиса в северном полушарии Земли стремятся сместить движущееся тело вправо, а в южном полушарии - влево по отношению к скорости движения тела v'.

По этой причине в северном полушарии правые берега рек более размытые, чем левые, а в южном полушарии, наоборот, более размыты левые берега; в северном полушарии