Курсовая работа: Пространство товаров. Цены

Но есть и некоторые отличия операций над векторами от операций над числами. Так, для любых чисел а и b ≠ 0 можно узнать, «во сколько раз» a больше b, т.е. найти а/b. Но для двух векторов это сделать, в общем, нельзя. Например, для Е = (7, 1) и N = (1, 1) нет такого λ, чтобы Е = λN.

Два вектора называются равными, если они равны покомпонентно, т.е. если равны их первые компоненты, вторые и т.д. Итак, если Х =(x₁ , … , x_n ), Y =(y₁ , … , y_n ), то Х = Y если и только если х_n = y_n . Как видно из определения равенства, лишь для векторов одинаковой размерности можно говорить о равенстве или неравенстве этих векторов. Для векторов разной размерности говорить об их равенстве бессмысленно.

Описанные действия с векторами были иллюстрированы на примере векторов-строк. Действия с векторами-столбцами точно такие же, в результате получаются, конечно, также векторы-столбцы. Векторы-строки и векторы-столбцы одинаковой размерности связаны операцией транспонирования . Она превращает вектор-строку в вектор-столбец и, наоборот, вектор-столбец в вектор-строку. Эта операция обозначается верхним индексом ^т . Пусть U= (2, 3), тогда U^T = (² ₃ ). Легко понять, что операция транспонирования, осуществленная последовательно дважды, дает исходный вектор: (X^T )^T = X, каков бы ни был вектор X — строка или столбец.

Скалярное произведение векторов. Пусть Х =(x₁ , … , x_n ), Y =(y₁ , … , y_n ) — векторы одинаковой размерности, тогда число x₁ y₁ + … + x_n y_n называется скалярным произведением векторов X и Y и обозначается X·Y. Приведем без доказательств (они очень просты) свойства скалярного произведения:

а) Х· = Y·X;

б) Х· (Y+ Z) = Х·У + Х·Z

в) Х· (λY) = λ (Х·Y) для любых векторов X, Y и любого числа λ.

2. Линейные пространства

Линейная зависимость и независимость векторов. Пусть Rⁿ обозначает множество всех n-мерных векторов-строк. Заметим, что это не просто множество — Rⁿ несет определенную структуру. Именно любой вектор Х∈ Rⁿ можно умножить на любое число λX и результат — вектор λX есть снова элемент множества R_n . Сумма двух и даже любого конечного числа векторов из Rⁿ снова есть элемент Rⁿ . Кроме того, операции умножения вектора на число и сложения векторов связаны друг с другом определенными соотношениями (см. п. 2).

Во множестве Rⁿ есть уникальный вектор 0 = (0, ..., 0). Его роль вполне аналогична роли числа 0 во множестве чисел. Так, 0·X = 0 и X+ 0 = Xдля любого Х∈ Rⁿ .

Вектор X, удовлетворяющий неравенству X > 0, называется неотрицательным . Неотрицательный вектор — это в точности тот, все компоненты которого неотрицательны. Вектор (2, 3) является неотрицательным, а вектор (-2, 4) — нет, ибо его 1-я компонента не является неотрицательным числом.

По всем этим причинам Rⁿ называют n-мерным числовым (или арифметическим) линейным пространством. Слово «числовое» в названии линейного пространства подчеркивает, что элементами такого пространства являются векторы, компоненты которых есть числа.

Вектор В = (b₁ , …, b_m ) называется линейной комбинацией векторов A = (a₁₁ , …, a_{m 1} ), …, An = (a_{1 n} , …, a_mn ) той же размерности, если найдутся числа х₁ , ..., х_n такие, что В = x₁ A₁ + ... + х_n А_n . Следовательно, чтобы узнать это, надо решить систему из m линейных алгебраических уравнений (СЛАУ) с n неизвестными:

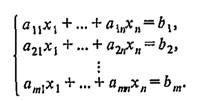
Узнаем, например, является ли вектор F = (1, 6) линейной комбинацией векторов H₁ = (1, 2), H₂ = (0, 2). Получаем совсем простую СЛАУ:

Ее решение: х₁ = 1, х₂ = 2. Следовательно, F = H₁ + 2H₂ .

Система векторов называется линейно зависимой если какой-то вектор системы есть линейная комбинация остальных векторов системы, и линейно независимой в противном случае, т.е. когда никакой вектор системы не является линейной комбинацией остальных векторов системы.

Например, система из трех вышеприведенных векторов F₁ , H₁ , H₂ линейно зависима, ибо F = H₁ + 2H₂

Пусть A — какая-нибудь система векторов, тогда ее подсистема ε называется базисом этой системы, если ε линейно независима, и любой вектор системы A есть линейная комбинация векторов из ε.

Пусть ε = (E₁ , …, E_n ). Если B∈A, то B = λ₁ E₁ +... + λ_n E_n при некоторых λ₁ , …, λ_n

Линейная комбинация λ₁ E₁ +... + λ_n E_n называется разложением вектора В по векторам E₁ ... E_n , а числа λ₁ , ..., λ_n называются коэффициентами этого разложения.

Эти коэффициенты называются координатами вектора в базисе ε.

3. Пространство товаров, цены

Под товаром понимается некоторое благо или услуга, поступившие в продажу в определенное время и в определенном месте. Будем считать, что имеется n различных товаров, количество i-го товара обозначается х_i тогда некоторый набор товаров обозначается X = = (x₁ ,…, х_n ). Как известно, упорядоченный набор n чисел называется n-мерным вектором, так что X есть n-мерный вектор. Вообще-то набор товаров надо считать вектором-столбцом, но по соображениям экономии места будем изображать его вектором-строкой. Будем рассматривать, как правило, только неотрицательные количества товаров, так что х_i ≥ 0 для любого i = 1, … ,n или Х≥ 0.

Множество всех наборов товаров называется пространством товаров С . Это множество называется пространством потому, что в нем можно сложить любые два набора и умножить любой набор товаров на любое неотрицательное число. Возможность умножения набора товаров на любое неотрицательное число отражает предположение о безграничной делимости и умножении товаров (т.е. товары устроены наподобие сахарного песка, а не авианосцев). Набор товаров можно трактовать, как корзину, в которой лежат эти товары в соответствующем количестве. Аналогично интерпретируются и операции с наборами товаров.

Решение потребителя о покупке определенного набора товаров математически - выбор конкретной точки в пространстве C.

Пример 2. Пространство товаров С представляет собой часть арифметического линейного пространства Rⁿ — так называемый неотрицательный октант, С = {X ∈ Rⁿ : X≥ 0}. Поэтому при работе с пространством товаров можно использовать структуру линейного пространства (соблюдая некоторые естественные ограничения). Так, для любого X Є С подмножество L_X = {λX: 0 ≤ λ} называется лучом , проходящим через X; для любых двух точек X, Y любая точка αХ + βY∈ С называется их линейной комбинацией , а множество [X, Y] = {αХ + βY: α, β ≥ 0, α + β = 1} называется отрезком , соединяющим X и Y. Подмножество W ≤ С является выпуклым, если вместе с любыми X,Y ∈ W весь соединяющий их отрезок лежит в W.

Предполагается, что каждый товар имеет цену. Все цены строго положительны. Пусть цена единицы i-го товара есть р_i , тогда Р = (p_i ,…,р_n ) есть вектор-строка цен.

Для набора товаров X и вектора цен Р их скалярное произведение РХ = р₁ x₁ + ... + р_n x_n есть число, называемое ценой набора X или его стоимостью, и будет обозначаться С(Х).