Курсовая работа: Проверка истинности моделей множественной регрессии
то можно говорить о статистической значимости и надёжности уравнения регрессии.
5. Сравнивая частные F – критерии фактические с пороговой константой Fтабл =4,21, делаем вывод: Fх2факт =12,95 > Fтабл , следовательно статистически подтверждена целесообразность включения в модель динамики валового накопления основного капитала, после числа студентов, т.к. этот фактор оказывает большее влияние.
Построение парных моделей регрессии
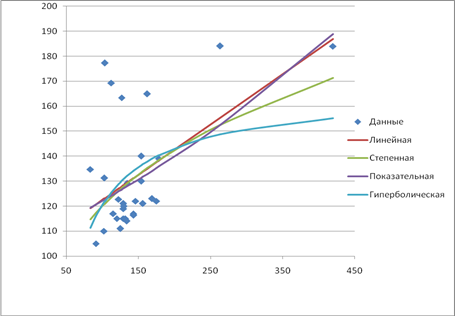
Представим данные полученные при построении парных моделей в таблице:
| Модель | Aср. | r (ρ) | Уравнение | Fфакт |
| Линейная | 10,89 | 0,5353 | у=102,38+0,201х1 | 11,24 |
| Степенная | 11,008 | 0,4934 | у=38,26×х1 0,2481 | 9,01 |
| Показательная | 10,47 | 0,5350 | у=106,53×1,001х1 | 11,23 |
| Гиперболическая | 12,59 | 0,3786 | у=165,92-4546,04/х1 | 4,68 |
Определение лучшей модели
1. Недопустимую ошибку аппроксимации имеют все 4 модели, однако у показательной модели она наименьшая, это говорит о том что линейная модель лучше аппроксимирует исходные данные чем остальные модели.
2. У линейной модели теснота связи самая сильная по сравнению с другими моделями. Это говорит о том, что показательная модель лучше подходит к нашим данным.
3. Проверив гипотезу о стат. значимости и надежности, получив значения Fфакт больше табличного во всех случаях, получаем, что все 4 уравнения являются стат. значимыми и надежными. Хотя линейная модель имеет наибольшее Fфакт по сравнению с другими моделями, это говорит о большей точности линейной модели.
По двум показателям линейная модель лучше остальных, это говорит о том, что линейная модель лучше аппроксимирует исходные данные. Однако множественная модель, на мой взгляд, лучше аппроксимирует данные, чем линейная, потому что множественная модель имеет допустимую ошибку аппроксимации и большую тесноту связи.
Проверка предпосылок МНК
1.Первую предпосылку проверим путём вычисления суммы значений остатков:
| x1 | x2 | y | x1x2 | yx1 | yx2 | y^x | y-y^x |
| 64 | 103 | 131,2 | 6592 | 8396,8 | 13513,6 | 126,48 | 4,72 |
| 50 | 169 | 123 | 8450 | 6150 | 20787 | 137,56 | -14,56 |
| 29 | 115 | 117 | 3335 | 3393 | 13455 | 122,09 | -5,09 |
| 22 | 103,4 | 177,3 | 2274,8 | 3900,6 | 18332,82 | 118,28 | 59,02 |
| 34 | 263,5 | 184,1 | 8959 | 6259,4 | 48510,35 | 154,21 | 29,89 |
| 195 | 162,2 | 164,9 | 31629 | 32155,5 | 26746,78 | 164,75 | 0,15 |
| 39 | 120 | 115 | 4680 | 4485 | 13800 | 125,11 | -10,11 |
| 42 | 178 | 139 | 7476 | 5838 | 24742 | 137,87 | 1,13 |
| 28 | 102 | 110 | 2856 | 3080 | 11220 | 119,17 | -9,17 |
| 42 | 112,4 | 169,3 | 4720,8 | 7110,6 | 19029,32 | 124,11 | 45,19 |
| 40 | 134 | 114 | 5360 | 4560 | 15276 | 128,25 | -14,25 |
| 34 | 125 | 111 | 4250 | 3774 | 13875 | 125,18 | -14,18 |
| 61 | 126,7 | 163,4 | 7728,7 | 9967,4 | 20702,78 | 130,86 | 32,54 |
| 42 | 156 | 121 | 6552 | 5082 | 18876 | 133,25 | -12,25 |
| 46 | 83,3 | 134,7 | 3831,8 | 6196,2 | 11220,51 | 118,80 | 15,90 |
| 15 | 420 | 184 | 6300 | 2760 | 77280 | 183,27 | 0,73 |
| 22 | 175 | 122 | 3850 | 2684 | 21350 | 133,29 | -11,29 |
| 33 | 129 | 119 | 4257 | 3927 | 15351 | 125,82 | -6,82 |
| 47 | 130 | 120 | 6110 | 5640 | 15600 | 128,79 | -8,79 |
| 54 | 154 | 140 | 8316 | 7560 | 21560 | 135,20 | 4,80 |
| 34 | 134,1 | 129,1 | 4559,4 | 4389,4 | 17312,31 | 127,08 | 2,02 |
| 32 | 132 | 115 | 4224 | 3680 | 15180 | 126,25 | -11,25 |
| 38 | 146 | 122 | 5548 | 4636 | 17812 | 130,37 | -8,37 |
| 58 | 143 | 117 | 8294 | 6786 | 16731 | 133,69 | -16,69 |
| 21 | 143,5 | 116,4 | 3013,5 | 2444,4 | 16703,4 | 126,49 | -10,09 |
| 51 | 122,6 | 122,7 | 6252,6 | 6257,7 | 15043,02 | 128,03 | -5,33 |
| 58 | 154 | 130 | 8932 | 7540 | 20020 | 135,99 | -5,99 |
| 36 | 129 | 115 | 4644 | 4140 | 14835 | 126,41 | -11,41 |
| 48 | 129 | 121 | 6192 | 5808 | 15609 | 128,78 | -7,78 |
| 32 | 91 | 105 | 2912 | 3360 | 9555 | 117,65 | -12,65 |
| сумма | 0,0000 |
2.Случайный характер остатков. Проверим графически:

Из графика зависимости остатков εi от теоретических значений результативного признака видно, что точки распределены случайно, следовательно, εi представляют собой случайные величины и МНК оправдан.
3. Наличие гомоскедастичности. Воспользуемся методом Гольдфельда – Квандта. Число исключаемых центральных наблюдений примем равным 8. Тогда в каждой группе будет по 11 наблюдений. Результаты расчетов представим в таблице:
| x1 | x2 | y | x1x2 | yx1 | yx2 | y^x | y-y^x | Ai | (y-y^x)^2 |
| 46 | 83,3 | 134,7 | 3831,8 | 6196,2 | 11220,51 | 132,15 | 2,55 | 1,8961 | 6,52 |
| 32 | 91 | 105 | 2912 | 3360 | 9555 | 128,41 | -23,41 | 22,2973 | 548,13 |
| 28 | 102 | 110 | 2856 | 3080 | 11220 | 127,98 | -17,98 | 16,3451 | 323,27 |
| 64 | 103 | 131,2 | 6592 | 8396,8 | 13513,6 | 139,08 | -7,88 | 6,0058 | 62,09 |
| 22 | 103,4 | 177,3 | 2274,8 | 3900,6 | 18332,82 | 126,24 | 51,06 | 28,7972 | 2606,87 |
| 42 | 112,4 | 169,3 | 4720,8 | 7110,6 | 19029,32 | 133,02 | 36,28 | 21,4308 | 1316,41 |
| 29 | 115 | 117 | 3335 | 3393 | 13455 | 129,22 | -12,22 | 10,4468 | 149,40 |
| 39 | 120 | 115 | 4680 | 4485 | 13800 | 132,65 | -17,65 | 15,3447 | 311,40 |
| 51 | 122,6 | 122,7 | 6252,6 | 6257,7 | 15043,02 | 136,51 | -13,81 | 11,2549 | 190,71 |
| 34 | 125 | 111 | 4250 | 3774 | 13875 | 131,48 | -20,48 | 18,4460 | 419,23 |
| 61 | 126,7 | 163,4 | 7728,7 | 9967,4 | 20702,78 | 139,87 | 23,53 | 14,4012 | 553,73 |
| 0,0000 | 15,1514 | 6487,74 |
| x1 | x2 | y | x1x2 | yx1 | yx2 | y^x | y-y^x | Ai | (y-y^x)^2 |
| 21 | 143,5 | 116,4 | 3013,5 | 2444,4 | 16703,4 | 119,32 | -2,92 | 2,5060 | 8,51 |
| 38 | 146 | 122 | 5548 | 4636 | 17812 | 124,14 | -2,14 | 1,7530 | 4,57 |
| 58 | 154 | 130 | 8932 | 7540 | 20020 | 131,22 | -1,22 | 0,9407 | 1,50 |
| 54 | 154 | 140 | 8316 | 7560 | 21560 | 130,25 | 9,75 | 6,9625 | 95,01 |
| 42 | 156 | 121 | 6552 | 5082 | 18876 | 127,90 | -6,90 | 5,7020 | 47,60 |
| 195 | 162,2 | 164,9 | 31629 | 32155,5 | 26746,78 | 166,75 | -1,85 | 1,1203 | 3,41 |
| 50 | 169 | 123 | 8450 | 6150 | 20787 | 133,47 | -10,47 | 8,5103 | 109,57 |
| 22 | 175 | 122 | 3850 | 2684 | 21350 | 128,35 | -6,35 | 5,2041 | 40,31 |
| 42 | 178 | 139 | 7476 | 5838 | 24742 | 134,04 | 4,96 | 3,5697 | 24,62 |
| 34 | 263,5 | 184,1 | 8959 | 6259,4 | 48510,35 | 155,95 | 28,15 | 15,2883 | 792,18 |
| 15 | 420 | 184 | 6300 | 2760 | 77280 | 195,01 | -11,01 | 5,9854 | 121,29 |
| 0,0000 | 5,2311 | 1248,57 |
Величина R=0,1924 (1248,57/6487,74), меньше табличного значения F-критерия, следовательно, наличие гомоскедастичности и отсутствие гетероскедастичности.
4.Отсутствие автокорреляции. Тест Дарбина–Уотсона:
| x1 | x2 | y | y^ | lу-у^l | (lу-у^l/у)*100 | у-у^ | ei-ei-1 | (ei-ei-1)^2 | (у-у^)^2 |
| 64 | 103 | 131 | 126,48 | 4,715497 | 3,594 | -4,715 | -4,7155 | 22,2 | 22,24 |
| 50 | 169 | 123 | 137,56 | 14,55865 | 11,836 | 14,559 | 19,27414 | 371,5 | 211,95 |
| 29 | 115 | 117 | 122,09 | 5,093094 | 4,353 | 5,093 | -9,46555 | 89,6 | 25,94 |
| 22 | 103 | 177 | 118,28 | 59,02032 | 33,288 | -59,020 | -64,1134 | 4110,5 | 3483,40 |
| 34 | 264 | 184 | 154,21 | 29,88682 | 16,234 | -29,887 | 29,13349 | 848,8 | 893,22 |
| 195 | 162 | 165 | 164,75 | 0,151302 | 0,092 | -0,151 | 29,73552 | 884,2 | 0,02 |
| 39 | 120 | 115 | 125,11 | 10,11485 | 8,796 | 10,115 | 10,26615 | 105,4 | 102,31 |
| 42 | 178 | 139 | 137,87 | 1,133281 | 0,815 | -1,133 | -11,2481 | 126,5 | 1,28 |
| 28 | 102 | 110 | 119,17 | 9,170267 | 8,337 | 9,170 | 10,30355 | 106,2 | 84,09 |
| 42 | 112 | 169 | 124,11 | 45,18646 | 26,690 | -45,186 | -54,3567 | 2954,7 | 2041,82 |
| 40 | 134 | 114 | 128,25 | 14,24733 | 12,498 | 14,247 | 59,43379 | 3532,4 | 202,99 |
| 34 | 125 | 111 | 125,18 | 14,17636 | 12,771 | 14,176 | -0,07097 | 0,0 | 200,97 |
| 61 | 127 | 163 | 130,86 | 32,53879 | 19,914 | -32,539 | -46,7152 | 2182,3 | 1058,77 |
| 42 | 156 | 121 | 133,25 | 12,25437 | 10,128 | 12,254 | 44,79316 | 2006,4 | 150,17 |
| 46 | 83,3 | 135 | 118,80 | 15,89794 | 11,802 | -15,898 | -28,1523 | 792,6 | 252,74 |
| 15 | 420 | 184 | 183,27 | 0,725914 | 0,395 | -0,726 | 15,17202 | 230,2 | 0,53 |
| 22 | 175 | 122 | 133,29 | 11,29077 | 9,255 | 11,291 | 12,01669 | 144,4 | 127,48 |
| 33 | 129 | 119 | 125,82 | 6,817621 | 5,729 | 6,818 | -4,47315 | 20,0 | 46,48 |
| 47 | 130 | 120 | 128,79 | 8,790167 | 7,325 | 8,790 | 1,972546 | 3,9 | 77,27 |
| 54 | 154 | 140 | 135,20 | 4,796736 | 3,426 | -4,797 | -13,5869 | 184,6 | 23,01 |
| 34 | 134 | 129 | 127,08 | 2,015804 | 1,561 | -2,016 | 2,780932 | 7,7 | 4,06 |
| 32 | 132 | 115 | 126,25 | 11,24923 | 9,782 | 11,249 | 13,26503 | 176,0 | 126,55 |
| 38 | 146 | 122 | 130,37 | 8,368454 | 6,859 | 8,368 | -2,88077 | 8,3 | 70,03 |
| 58 | 143 | 117 | 133,69 | 16,68649 | 14,262 | 16,686 | 8,318035 | 69,2 | 278,44 |
| 21 | 144 | 116 | 126,49 | 10,08938 | 8,668 | 10,089 | -6,59711 | 43,5 | 101,80 |
| 51 | 123 | 123 | 128,03 | 5,32814 | 4,342 | 5,328 | -4,76124 | 22,7 | 28,39 |
| 58 | 154 | 130 | 135,99 | 5,992662 | 4,610 | 5,993 | 0,664522 | 0,4 | 35,91 |
| 36 | 129 | 115 | 126,41 | 11,40967 | 9,921 | 11,410 | 5,417008 | 29,3 | 130,18 |
| 48 | 129 | 121 | 128,78 | 7,777864 | 6,428 | 7,778 | -3,63181 | 13,2 | 60,50 |
| 32 | 91 | 105 | 117,65 | 12,65349 | 12,051 | 12,653 | 4,875628 | 23,8 | 160,11 |
| 19110,43 | 10002,65 |
Исходя из статистики Дарбина-Уотсона, можно сделать вывод, что автокорреляция отсутствует, так как 1,91 находится в промежутке (1,339;2,661) (d2 ; 4-d2 ). Следовательно, значения остатков распределены независимо друг от друга. Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.
Таким образом, не все предпосылки выполнились, это говорит о недостаточной надежности уравнения множественной регрессии. Возможно, можно было бы и получить надежную модель, если исключить из данных страны значение динамики ВВП, которых сильно отличается от других.