Курсовая работа: Радиотелеметрическая система с частотным разделением товаров
где 
. Можно показать, что средняя удельная мощность ФМ колебания равна 
, т.е. мощности несущей в отсутствие модуляции.
1.3 Линейная частотная модуляция
Модулированное гармоническое колебание в этом случае имеет следующий вид:
, ( 12)
где 
- коэффициент, характеризующий свойства модулятора при ЧМ. Представим выражение ( 12)следующим образом:
( 13)
где 
- парциальная девиация частоты за счет составляющей модулирующего колебания с частотой 
. Зависимость 
от 
называется модуляционной характеристикой при ЧМ. Учитывая, что фаза и частота связаны соотношением
( 14)
Получим
, ( 15)
где 
, 
. Т.е. спектры ЧМ и ФМ колебаний совпадают, если под индексом модуляции понимать .
2. Характеристики группового тракта
Групповым трактом является часть РТМ системы, по которой проходит групповой сигнал (с выхода сумматора до разделителя) (рисунок 3)
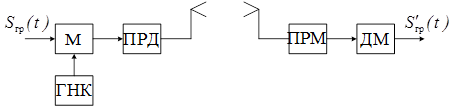
Рисунок 3
Групповой тракт описывается:
амплитудной характеристикой 
;
амплитудно-частотной характеристикой;
фазо-частотной характеристикой.
Наибольшее влияние на качество передачи информации имеет амплитудная характеристика (АХ). Нелинейность АХ вызывает появление дополнительных спектральных составляющих и как следствие межканальных помех. Для получения неискаженной модуляции во второй ступени необходимо, чтобы групповой сигнал не превышал определенного уровня (рисунок 4).
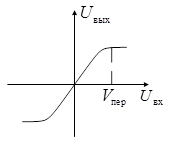
Рисунок 4
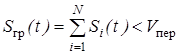, ( 16)
где 
- число каналов, 
- амплитуда модулированного колебания i-ой поднесущей.
Определим вероятность того, что групповой сигнал 
превысит уровень 
. Полагаем, что фазы всех поднесущих независимы и распределены равновероятно на интервале 
. При 
, в силу центральной предельной теоремы, распределение 
хорошо описывается нормальным законом (рисунок 5)
Рисунок 5
, ( 17)
где 
- дисперсия процесса . Дисперсия процесса при амплитудной модуляции поднесущих с 
, как следует из формулы ( 4), равна