Курсовая работа: Рамочный датчик угла

Выходное напряжение датчика

U_1I =E₁ -E_{2 ,} (1)

где и Е₂ — э. д. с, наведенные соответственно в левой и правой сигнальных катушках.

Определим величины и Е₂ , предположив, что сигнальные катушки имеют прямоугольную форму, а кронштейн с сигнальными катушками повернулся по часовой стрелке на малый угол β так, что линейное перемещение рамки слева направо составляет величину ρβ (см. рисунок 4).

Рассмотрим контур dx, находящийся на расстоянии х от торца полюса. Поток, пронизывающий этот контур, равен:

Ф_х = В S_x, (2)

где B= ab — индукция в зазоре; S_x =bx — площадь, заполненная потоком .

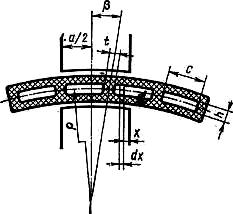
Рисунок 4 - К выводу аналитического выражения характеристики датчика с подвижной катушкой

Подставляя значения В и S_x в (2), получаем

(3)

Число витков сигнальной катушки, содержащихся в контуре dx, равно:

w_dx =, (4)

где k₃ — коэффициент заполнения окна сигнальной катушки; h — толщина сигнальной катушки; q — сечение провода сигнальной катушки.

Элементарная э.д.с, наводимая в контуре dx, равна:

πf (5)

Подставляя (3) и (4) в (5), получим

πfФxdx

Интегрируя выражение dE₂ , получим

2 πf(ρβ) (6)

Аналогично определяется величина:

πf (ρβ) (7)

Потоки выпучивания также наводят э.д.с. в сигнальных катушках. Обозначив эти э.д.с. через Е_1в и Е_2в , получим:

(8)

Точно рассчитать э.д.с. Е_1в и Е_2в трудно, так как сложно точно учесть распределение и интенсивность потоков выпучивания. Ввиду меньшей интенсивности потоков выпучивания по сравнению с рабочим потоком приближенно считаем:

Е_1в Е_2в (9)

Подставляя (7) и (8) в (9), а последнее,с учетом приближенного равенства (10) в (1), получаем

-U = 2 πf ρ(a-t)β (10)