Курсовая работа: Расчет антенны для земной станции спутниковой системы

Помимо аналитического вычисления эксцентриситета малого зеркала гиперболы, приведем графическое. На рисунке 2.1 представлены графики, показывающие значения изменения эксцентриситета образующей гиперболы в зависимости от углов (Ψ₀ ) и (φ₂ ).

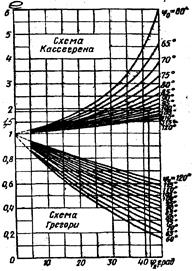
Рисунок 2.1 – зависимость эксцентриситета от углов (Ψ₀ ) и (φ₂ ).

Из графика видно, что при углах Ψ₀ =103⁰ и φ₂ =41⁰ значение эксцентриситета близко к полученному при аналитических вычислениях результату: .

Для дальнейшего расчета нам необходимо определить фокусное расстояние большого (F) и малого (f) зеркал. Это можно сделать, используя следующее соотношение:

;

Из приведенного выше соотношения видно, что F_э определится как:

;

Теперь рассчитаем фокусное расстояние малого зеркала, при этом формула для его определения выглядит следующим образом:

;

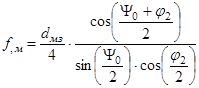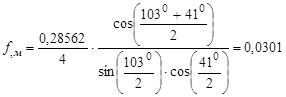
Как известно, разность расстояний от фокусов до произвольной точки на поверхности гиперболоида постоянна, т.е. , где 2а – это расстояние между его вершинами. Расстояние между фокусами гиперболоида . При этом эксцентриситет образующей гиперболы равен . Наглядно расстояние 2а и 2С представлены на рисунке 2.2.

Рисунок 2.2 – графическое представление расстояний 2С и 2а

Теперь мы можем отыскать численные значения расстояний 2С и 2а. Для этого используем выражение:

;

;

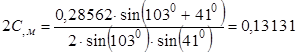
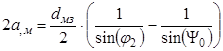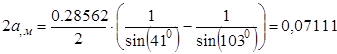
Выполним проверку на условие , условие удовлетворено, следовательно, расстояния найдены, верно.

На завершающем этапе расчета данного параграфа нам необходимо определить диаметр облучателя:

;

Таким образом, диаметр облучателя можно определить как:

;

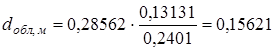
При этом условие выполняется.

2.4 Расчет профилей большого и малого зеркал