Курсовая работа: Расчет элементов ферменно стержневой конструкции

где

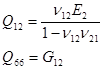(1.3)

Составим матрицу Q 1 для слоев под углом 0⁰

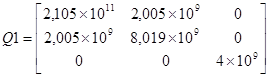, (Па)

Составим матрицу Q 2 для верхнего нижнего слоев

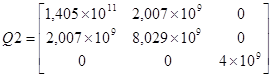, (Па)

Приведенные зависимости относятся к частному случаю, когда оси нагружения x и y совпадают с осями упругой симметрии ортотропного материала 1 и 2. В общем случае эти оси не совпадают, и уравнения состояния отдельных слоев должны быть трансформированы в произвольных осях по следующей схеме:

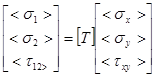(1.4)

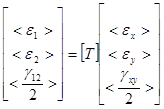(1.5)

Матрица трансформации имеет следующий вид:

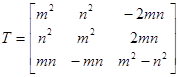(1.6)

где m = cos ( α ) и n = sin (α )

матрица тансформации для α = 0

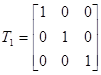
Матрица трансформации для α = 80

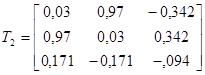
Матрица трансформации для α = -80

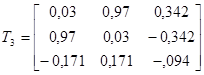
Используя зависимости (2), (4) и (5), уравнения состояния слоя впроизвольных осях x и y можно записать в следующем виде:

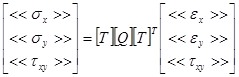(1.7)

Введем следующие обозначения

(1.8)

где Θ _j – относительная толщина слоя

Закон деформирования для пакета слоев:

(1.9)

где 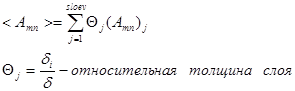(1.10)

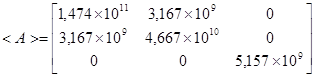, (Па)

Получаем выражения технических деформативных характеристик слоистых материалов через упругие характеристики <A_mn >, а следовательно, через соответствующие характеристики отдельных слоев: