Курсовая работа: Расчет и конструирование катодного узла
Рисунок 2.3.2 – Схема подогревателя
Верхняя часть подогревателя есть ничто иное, как спираль Архимеда. В полярной системе координат уравнение Архимедовой спирали выглядит так: 
. Из аналитической геометрии известно, что если гладкая кривая задана уравнением 
, то длина дуги этой кривой выражается интегралом: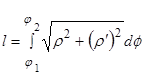 
, где f1 и f2 - значения полярного угла φ в концах дуги. Для спирали Архимеда этот интеграл запишется как
.
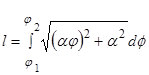Интеграл табличный и равен:
.
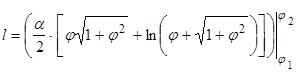Зная длину дуги (длина подогревателя), подбираем параметры спирали так, чтобы они соответствовали геометрическим размерам катода. Для этого воспользуемся программным пакетом Mathcad, положив, что 
и f1 =0. Методом подбора установим, что оптимальными значениями a и f2 будут a=0.125 и f2 =3.5p. Внешний вид полученной спирали представлен на рисунке 2.3.3.
Рисунок 2.3.3 – Внешний вид спирали
2.4 Расчет охлажденных концов держателя
В качестве материала держателей выберем цирконий, так как он обладает низкой теплопроводностью. Рассчитаем длину держателей:
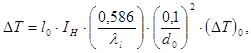[1]
Отсюда:
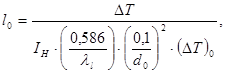
где 
- значение 
для 
см, 
см, 
А, зависящие от температуры 
. При =2500
, 
, [1]
, [1] - теплопроводность материала ввода;
- ток накала;
- диаметр держателя;
разница между температурой держателей и температурой окружающей среды. Приняв температуру окружающей чреды за 300 К получим 
;
Таким образом:
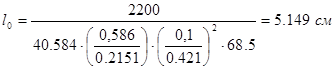
2.5 Расчет мощности потерь на охлажденных концах
Рассчитаем потери мощности на охлаждённых концах:
где 
- коэффициент излучения для циркония;
=5.62
- постоянная Стефана-Больцмана,
- температура держателя,
- длина держателей,
- диаметр держателей.
.