Курсовая работа: Расчет на прочность крыла большого удлинения и шасси транспортного самолета АН–148
, где 
- хорда крыла.
Массовую нагрузку от веса топлива распределяем пропорционально площадям поперечного сечения топливных баков
, где 
- удельный вес топлива.
где 
- вес топлива (для самолёта АН 148 
).
Суммарная погонная нагрузка на крыло находится по формуле:
.
Начало координат поместим в корне крыла, сечения нумеруем от корня в направлении конца крыла, начиная с 
.
Результаты расчетов заносим в таблицу .
Таблица
 | z, м | b(z), м |  |  |  |  , кг/м |  , кг/м |  , кг/м |  , кг/м |
| 0 | 0 | 4,93 | 1,3435 | -0,060421 | 1,283079 | 4048,02 | 505,33 | 2187,441 | 1355,25 |
| 0,1 | 1,462 | 4,559 | 1,3298 | -0,044994 | 1,284806 | 4053,46 | 467,30 | 1870,603 | 1715,56 |
| 0,2 | 2,924 | 4,188 | 1,2908 | -0,031625 | 1,259175 | 3972,60 | 429,27 | 1578,541 | 1964,79 |
| 0,2 | 2,924 | 4,188 | 1,2908 | -0,031625 | 1,259175 | 3972,60 | 429,27 | 0 | 3543,33 |
| 0,3 | 4,386 | 3,817 | 1,2228 | -0,018512 | 1,204288 | 3799,44 | 391,24 | 0 | 3408,20 |
| 0,4 | 5,848 | 3,446 | 1,1484 | 1,141972 | 3602,84 | 353,22 | 0 | 3249,62 | |
| 0,4 | 5,848 | 3,446 | 1,1484 | 1,141972 | 3602,84 | 353,22 | 1068,742 | 2180,88 | |
| 0,5 | 7,31 | 3,075 | 1,057 | 0,006428 | 1,063428 | 3355,03 | 315,19 | 851,0063 | 2188,84 |
| 0,6 | 8,772 | 2,704 | 0,9571 | 0,018769 | 0,975869 | 3078,79 | 277,16 | 658,0454 | 2143,59 |
| 0,7 | 10,234 | 2,333 | 0,8538 | 0,028539 | 0,882339 | 2783,71 | 239,13 | 489,86 | 2054,72 |
| 0,8 | 11,696 | 1,962 | 0,743 | 0,03471 | 0,77771 | 2453,62 | 201,11 | 346,45 | 1906,06 |
| 0,9 | 13,158 | 1,591 | 0,6091 | 0,035996 | 0,645096 | 2035,23 | 163,08 | 227,8153 | 1644,34 |
| 0,95 | 13,889 | 1,4055 | 0,4593 | 0,032139 | 0,491439 | 1550,45 | 144,06 | 177,7887 | 1228,60 |
| 1 | 14,62 | 1,22 | 0 | 0 | 0 | 0,00 | 0,00 | 0 | 0 |
Строим эпюры функций , 
и 
(рис. 7)
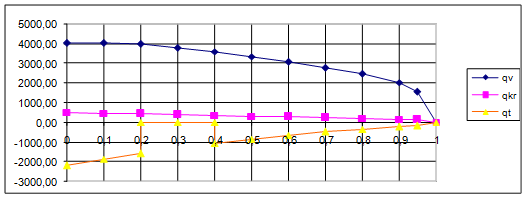
Рис. 7
Суммарная погонная нагрузка на крыло :
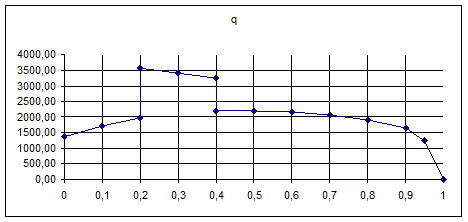
Построение эпюр поперечных сил, изгибающих и приведенных моментов.
При определении закона распределения поперечных сил и изгибающих моментов по длине крыла вначале находим функции 
и 
от воздействия распределенной нагрузки 
. Для этого табличным способом вычисляем интегралы методом трапеций.
, 
,
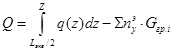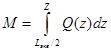Расчет производим по следующим формулам:
;
; 
,
, 
.
Аналогично рассчитываем величины изгибающих моментов:
; 
;
,
Полученные результаты заносим в таблицу 2.
Таблица 2
| z,м | ΔQ, кг | Q, кг | ΔM, кгм | M, кгм |
| 0 | 0 | 2244,77 | 20592,41 | 196758,3 | 1016728 |
| 0,1 | 1,462 | 2690,34 | 18347,64 | 172115,8 | 819969,8 |
| 0,2 | 2,924 | 2969,13 | 15657,30 | 152033,9 | 647854 |
| 0,3 | 4,386 | 3127,09 | 12688,17 | 130883,4 | 495820,1 |
| 0,4 | 5,848 | 3194,27 | 53414,20 | 121865,8 | 364936,7 |
| 0,5 | 7,31 | 3167,01 | 43712,46 | 87477,02 | 243070,9 |
| 0,6 | 8,772 | 3068,96 | 34081,88 | 66035,43 | 155593,9 |
| 0,7 | 10,234 | 2895,33 | 24644,21 | 57833,87 | 89558,46 |
| 0,8 | 11,696 | 2595,34 | 15538,14 | 24598,34 | 31724,59 |
| 0,9 | 13,158 | 1602,68 | 6337,4565 | 7126,248 | 7126,248 |
| 1 | 14,62 | 0 | 0 | 0 | 0 |
Необходимо учесть воздействие сосредоточенных массовых сил 
:
(кг);
, 
;
,