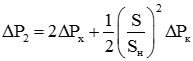(7)

то равенство будет иметь место при нагрузке, равной

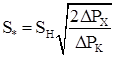. (8)

3. ЗАДАНИЕ НА РАСЧЁТ

1.Для заданной максимальной нагрузки выбрать необходимую мощность трансформаторов, параметры которых представлены в табл.1.

2. Для выбранного трансформатора построить зависимости суммарных потерь от нагрузки для одного трансформатора и двух, включенных параллельно.

3. Для графика нагрузки в относительных единицах, приведенного на рис.8, и заданной максимальной мощности определить число включенных трансформаторов, обеспечивающее в течение суток минимальные потери электроэнергии.

4.Рассчитать зависимость КПД трансформатора от нагрузки при заданном значении .

Таблица 1

Параметры трансформаторов

№	Тип и мощность, кВА	Рх , кВт	Рк , кВт
1	ТМ–25	0.125	0.6
2	ТМ–40	0.180	0.88
3	ТМ–63	0.265	1.28
4	ТМ–100	0.365	1.97
5	ТМ–160	0.540	2.65
6	ТМ–250	0.780	3.7
7	ТМ–400	1.080	5.5
8	ТМ–630	1.680	7.6

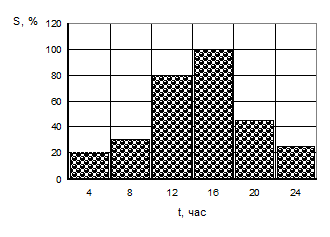
Рис.8. График нагрузки в процентах

4.РЕШЕНИЕ

Задана максимальная нагрузка . Выбор мощности трансформаторов осуществляется по двум условиям:

1.В нормальном режиме работы суммарная номинальная мощность трансформаторов должна превышать .

2.В аварийном режиме при отключении одного трансформатора оставшийся в работе должен обеспечить (с учетом 40% перегрузки) передачу мощности .

Следовательно условия выбора трансформаторов можно записать в виде:

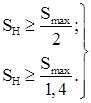
Для заданной мощности эти условия будут иметь вид

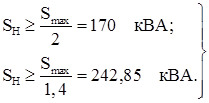
По табл. 1 выбирается трансформатор .

По формулам (6) и (7) рассчитываются зависимости потерь от нагрузки при одном и двух, параллельно работающих трансформаторах. Результаты расчета сводятся в табл. 2.

Таблица 2

Расчет потерь мощности в трансформаторе

S, кВА	, кВт	, кВт
0	0,78	1,56
20	0,80	1,57
40	0,87	1,61
60	0,99	1,67
80	1,16	1,75
100	1,37	1,86
120	1,63	1,99
140	1,94	2,14
160	2,30	2,32
180	2,70	2,52
200	3,15	2,74
220	3,65	2,99
240	4,19	3,26
260	4,78	3,56
280	5,42	3,88
300	6,11	4,22
320	6,84	4,59
340	7,62	4,98
360	8,45	5,40
380	9,33	5,83
400	10,25	6,30
420	11,22	6,78
440	12,24	7,29
460	13,31	7,82
480	14,42	8,38
500	15,58	8,96

По данным табл. 5 строятся зависимости суммарных потерь от нагрузки, приведенные на рис.9.

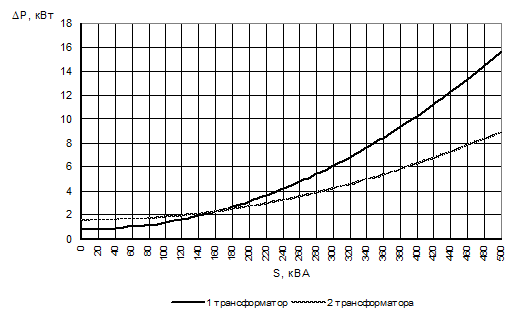
Рис.9. Зависимости потерь от нагрузки

График в относительных единицах, приведенный на рис. 8, пересчитывается в именованные единице по формуле

, ,

где i –номер ступени графика нагрузки. Результаты расчетов сводятся в табл.3.

Таблица 3

График нагрузки в именованных единицах

Номер ступени графика		, кВА
1	20	96
2	30	144
3	80	384
4	100	480
5	45	216
6	25	120

По данным табл. 3 строится график нагрузки (кВА), показанный на рис.10.

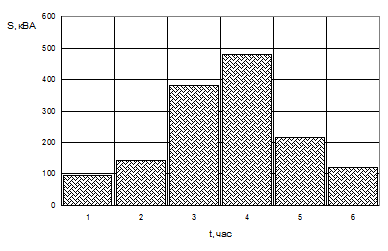
Рис. 10. График нагрузки в именованных единицах

По формуле (8) определяется мощность , при которой выполняется равенство :

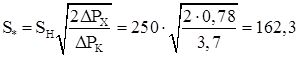кВА.

Число включенных трансформаторов, обеспечивающих минимальные потери энергии в течении суток, определяется по алгоритму:

.

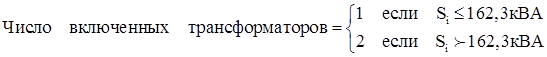Результаты выбора представляются в виде графика, приведенного на рис.11.

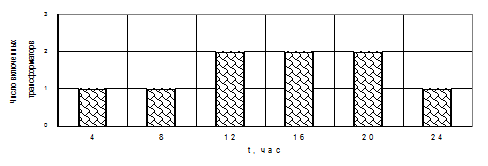
Рис.11. Оптимальное число включенных трансформаторов

Зависимость коэффициента полезного действия от нагрузки рассчитывается по формуле (4). Коэффициент мощности принимается равным 0,8. Результаты расчета сводятся в табл.4.

Таблица 4

Расчет КПД трансформатора

№	S, кВА	, %
1	0	0
2	1	50.63
3	5	83.66
4	10	91.05
5	20	95.22
6	30	96.64
7	40	97.34
8	50	97.73
9	60	97.97
10	70	98.12
11	80	98.22
12	90	98.28
13	100	98.31
14	110	98.33
15	114,75	98.33
16	120	98.33
17	130	98.32
18	140	98.30
19	150	98.27
20	160	98.24
21	170	98.20
22	180	98.16
23	190	98.12
24	200	98.07
25	210	98.02
26	220	97.97
27	230	97.92
28	240	97.86
29	250	97.81

По данным строится зависимость КПД от нагрузки, представленная на рис. 12. На рис. 13 показан фрагмент этой зависимости в области максимально возможно КПД.

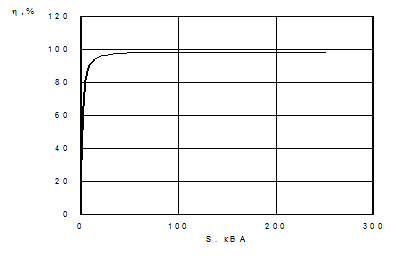
Рис.12. Зависимость КПД от нагрузки

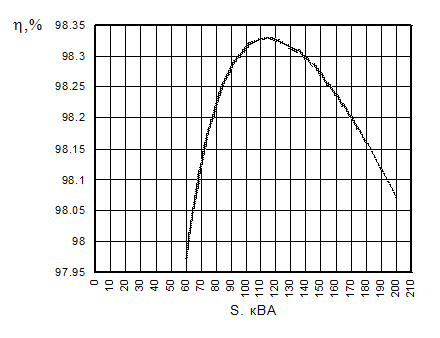
Рис.13. Фрагмент зависимости КПД от нагрузки в области максимального