Курсовая работа: Расчёт спиральной антенны круговой поляризации
Главный лепесток ДН витка спирали в плоскости Е уже, чем в плоскости Н. Это связано с тем, что элементарный излучатель витка - диполь Герца в плоскости Н излучает ненаправленно, а в плоскости Е вдоль оси не излучает.
В суммарном поле витка спирали, имеющем круговую поляризацию, плоскости Е и Н вращаются вокруг оси Z с частотой поля. Поэтому рассматриваются диаграммы направленности по составляющим Еθ и Еφ.
Эти диаграммы направленности определяются следующими выражениями [1]:
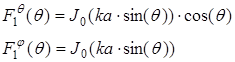
где J0 - функция Бесселя нулевого порядка; k - волновое число свободного пространства; R – радиус спирали.
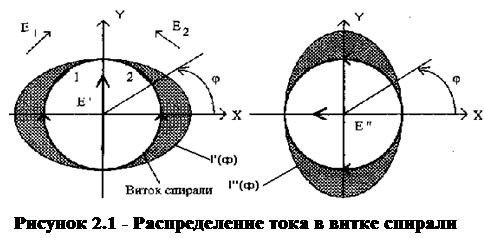 |
Вдоль системы витков распространяется бегущая волна тока, поэтому устанавливается линейное фазовое распределение. Поля всех витков в направлении оси Z (в направлении вектора фазовой скорости волны тока) складываются с одинаковыми фазами, в противоположном направлении - компенсируют друг друга. В результате спиральная антенна на волне Т 1формирует поле с осевой диаграммой направленности.
Аналогично, рассматривая распределение тока в витке спирали на волне Т2, можно показать, что виток спирали имеет коническую ДН. В элементах витка, расположенных диаметрально противоположно, токи противофазны, поэтому их суммарное поле на оси спирали равно нулю. Под некоторым углом к оси поля этих элементов уже сдвинуты по фазе за счет разности хода, и их суммарное поле не равно нулю. То же самое наблюдается на всех волнах Тm. Причем с ростом номера m растет число боковых лепестков ДН, а направление главного максимума приближается к оси спирали - угол Θm уменьшается.
В режиме Т0, когда резонирует нулевая пространственная гармоника (m=0), ток на протяжении всего витка спирали имеет одинаковую фазу (одинаковое направление). Поэтому такой виток эквивалентен магнитному диполю, не излучающему вдоль оси витка. Диаграмма направленности антенны в режиме Т0 имеет форму тороида.
Гармоника с номером m резонирует в поле спирали, если на периметре цилиндра спирали укладывается m длин волн, т.е. 2πR=mλ или
![]()
Подробный анализ типов волн в спиральной линии показывает, что условие (6) определяет среднюю длину волны рабочего диапазона, в котором существует волна Тm.Таким образом для создания в спиральной линии волны Т1, которая удовлетворяет требованиям, предъявляемым к антенне в данной работе, необходимо, чтобы ![]()
Диаграмму направленности и КНД спиральной антенны можно приближенно рассчитать по формулам, полученным аналитически для линейной антенной решетки с равномерным амплитудным и линейным фазовым распределением возбуждения; более точно - численно, предварительно решив внутреннюю задачу. Можно также расчет антенны и ее параметров произвести по эмпирическим формулам, полученным в результате обработки большого числа экспериментальных результатов.
Аналитический метод заключается в следующем. Регулярную спиральную антенну с числом витков n можно считать линейной антенной решеткой. Диаграмма направленности такой решетки по составляющим eθ и Еφ определяется выражением [2]:
![]()
Диаграммы направленности одного излучателя - витка спирали описываются формулами (5). Множитель системы Fc(θ) для решетки с равномерным амплитудным и линейным фазовым распределением определяется выражениями [2]:
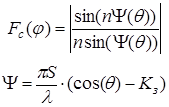
где S - расстояние между соседними излучателями (шаг спирали).
Коэффициент замедления 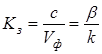 , где β - коэффициент фазы замедленной волны, распространяющейся вдоль оси спирали.
, где β - коэффициент фазы замедленной волны, распространяющейся вдоль оси спирали.
Аналитическое решение задачи по определению типов волн в регулярной (бесконечной) спирали показывает, что коэффициент замедления превышает единицу на 0,01-0,001 и его можно считать равным 1. В этом случае можно применить выражение КНД, полученное для линейной антенны в режиме осевого излучения [2]:
![]()
где l=n×S - осевая длина спирали (длина направителя).
Выражение (10) дает заниженное значение КНД. Это связано с тем, что в спирали конечной длины коэффициент замедления больше. Приближенно его определяют из условия синфазного сложения полей всех витков в направлении оси спирали (хотя это и недостаточно обоснованно), что приводит к следующему выражению [3]:
![]()
Это значение коэффициента замедления при L/λ > 1,5 близко к оптимальному в линейной антенне в режиме осевого излучения и равному [2]:
![]()
При оптимальном коэффициенте замедления КНД определяются выражениями [2]
![]()
которые дают более точные значения.
Выражения (8), (9) справедливы при целом числе витков спирали N. Если N не целое, спиральную антенну для расчета ДН считают линейной антенной с равномерным амплитудным и линейным фазовым распределением длиной L. В этом случае множитель системы определяется выражением [2]: