Курсовая работа: Расчёт спиральной антенны круговой поляризации

где

Формулы (8), (9) и (14), (15) дают близкие результаты, если N>5.

Аналитический метод расчета диаграммы направленности и КНД спиральной антенны является приближенным в силу использованных выше допущений (пренебрежение волнами, излучаемыми возбудителем и концом направителя) и неточного значения коэффициента замедления. Кроме того, в таком расчете не учитывается металлический экран диаметром Dэ » (0,6 - 0,7)λ., который всегда применяется для уменьшения заднего излучения и повышения эффективности возбуждения замедленной волны в спирали. Поэтому часто для расчета КНД используют следующее эмпирическое выражение [4], в котором k -волновое число свободного пространства:

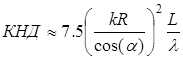
Входное сопротивление в широкой полосе частот имеет малую реактивную часть. Активное сопротивление приближенно определяется выражением:

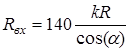
Основным режимом регулярной спиральной антенны является режим осевого излучения, наблюдаемый на волне T1. Поэтому рассмотрим диапазонные свойства в этом режиме [1].

Волна T1 в однозаходной спиральной линии существует в диапазоне длин волн λmax-λmin, которые связаны с волновым числом свободного пространства k и радиусом спирали R соотношением:. Получены следующие выражения для значений (kR)min и (kR)max:

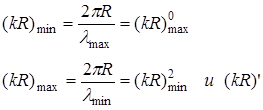
где (kR)0max ограничивает значение kR со стороны меньших значений и является верхней границей области существования волны Т0;

kR' ограничивает область существования волны Т1 в которой резонирует пространственная гармоника с m=1 (обеспечивается режим осевого излучения);

(kR)2min ограничивает со стороны меньших значений область существования волны Т2.

Указанные значения kR определяются выражениями:

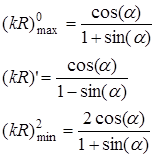
На рисунке 2.2 показаны зависимости приведенных значений kRот угла намотки спирали а. Область значений kR и α, в которой выполняются условия (19), (20), заштрихована. В этой области существует волна Т1, и в ней резонирует пространственная гармоника с номером m=1, т.е. в спиральной антенне существует режим осевого излучения. Как видно, эта область имеет максимальную ширину по шкале kR = 2πR/λ (следовательно, по шкале длин волн λ) при некотором оптимальном угле намотки спирали αопт. Максимальная ширина этой области ограничена значениями kRmiu и kRmax, а по шкале длин волн значениями λmax и λmin. Из условия равенства значений kR' и (kR)min при α=αonT нетрудно получить αопт=19,5°. Значения, ограничивающие область режима осевого излучения, получаются равными:

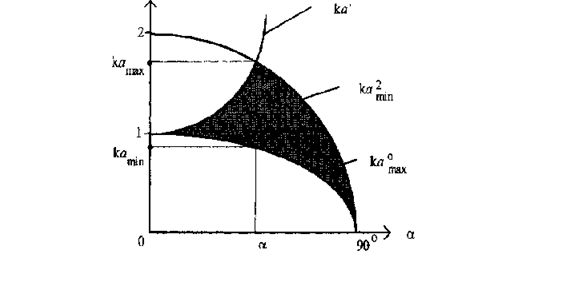??? ???? λmin≈4.5R; λmax≈9R ??????????? ?????????? ?? ??????? ?????????? ??????

Рисунок 2.2 - Область режима осевого излучения спиральной антенны

2. Среднее в диапазоне значение длины волны получается равным периметру цилиндра спирали 2πR.

Для определения КСВ и коэффициента усиления антенны в литературных источников приводится ряд формул, в контексте решения поставленной задачи воспользуемся следующими [3]:

,

где К0- коэффициент отражения:

Антенна будет возбуждаться коаксиальным кабелем РК-2-11 (50 Ом). Параметры этой коаксиальной линии: диаметр внутренней жилы – 0.67 мм, диаметр диэлектрика – 2 мм, внешний диаметр – 3.9 мм[7]. Для подключения будет использоваться SMA разъём.

Вид SMAразъёма иллюстрирует рисунок 2.3.

Рисунок 2.3 – Вид SMA разъёма

Поскольку обычно волновое сопротивление фидера фиксировано, а входное сопротивление спирали может быть различным, то в этом случае надо применить согласующее устройство СВЧ. Входное сопротивление спиральной антенны в режиме осевого излучения остаётся чисто активным, так как в этом режиме в проводе спирали устанавливается режим бегущей волны [5]. Поэтому для согласования можно применить конусообразный переход (рисунок 2.4) из коаксиальных линий передачи.

Рисунок 2.4 – Коаксиальный трансформатор

Если длину конусной части () взять равной l/4, то этот переход работает как четвертьволновый трансформатор для согласования линии с разным волновым сопротивлением[6].

Волновое сопротивление конусной части линии, должно быть:

[6], где

-волновое сопротивление конусной части перехода

-волновое сопротивление подводящего фидера